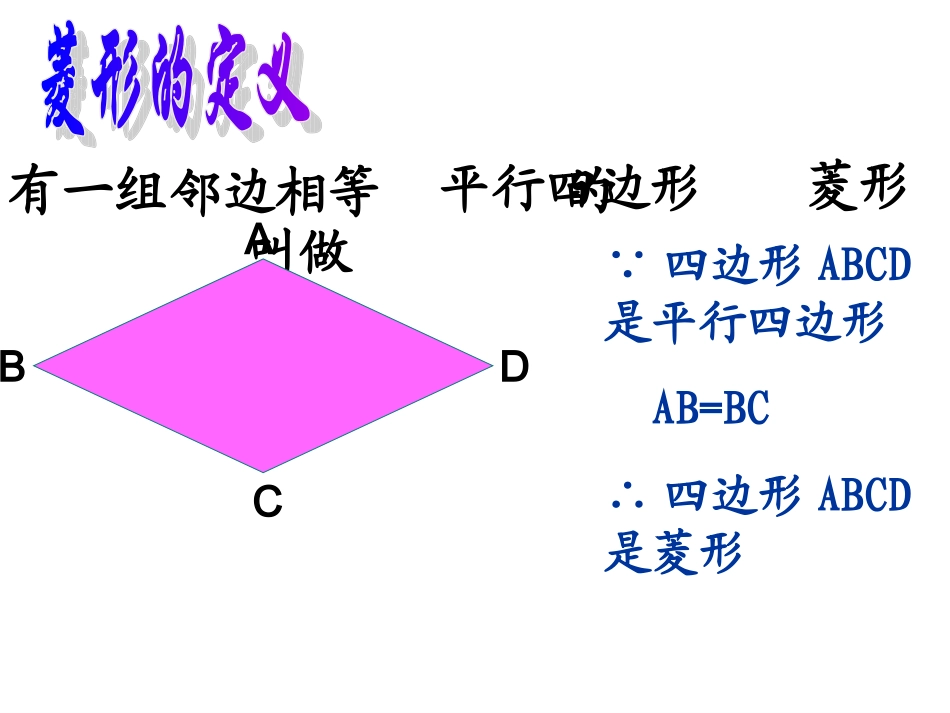
§18.2.2菱形的判定菱形活动一复习与回顾:想一想:1.菱形的定义?2.菱形哪些性质?有一组的叫做邻边相等平行四边形ADCB∵四边形ABCD是平行四边形AB=BC∴四边形ABCD是菱形菱形ADCBO边角对角线对称性菱形的两组对边平行且相等几何语言∵四边形ABCD是菱形∥=∴ADBCABCD∥=菱形的四条边相等∴AB=BC=CD=DA菱形的两组对角分别相等∴∠DAB=DCB∠∠ADC=ABC∠菱形的邻角互补∴∠DAB+ABC=∠180°菱形的两条对角线互相平分∴OA=OC;OB=OD菱形的两条对角线互相垂直,每一条对角线平分一组对角。∴ACBD⊥∠1=2∠∠3=4∠∠5=6∠∠7=8∠菱形是轴对称图形,有2条对称轴,是两条对角线所在的直线。12435768活动二想一想同学们想一想,我们在学习平行四边形的判定和矩形的判定时,我们首先想到的第一种方法是什么?那么类比着它们,菱形的第一种判定方法是什么?一组邻边相等的平行四边形是菱形.根据定义得:ABCD.,是菱形中在ABCDADABABCD还有其它方法吗?探究一用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?猜想:猜想:对角线互相垂直的平行四边形是菱形.命题:对角线互相垂直的平行四边形是菱形.ABCD已知:在中,AC⊥BDABCDABCD求证:是菱形证明:∴ABCD是菱形又∵ACBD;⊥∵四边形ABCD是平行四边形∴OA=OC∴BA=BCO定理:对角线互相垂直的平行四边形是菱形.(一组邻边相等的平行四边形是菱形)判定方法2:对角线互相垂直的平行四边形是菱形ACBD⊥∵在□ABCD中,AC⊥BD∴□ABCD是菱形ABCD菱形ABCDABCD□ABCD数学语言例1如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AC=8,DB=6(1)AC、BD互相垂直吗?为什么?(2)四边形ABCD是菱形吗?为什么?ABCDO∴四边形ABCD是菱形.(对角线互相垂直的平行四边形是菱形)∴OA=OC=4OB=OD=3(平行四边形的对角线互相平分)解:∵AB=5∴∴AC⊥BD090∴∠AOB=(2)∵四边形ABCD是平行四边形AC⊥BD(1)∵四边形ABCD是平行四边形AB2=OA2+OB2(勾股定理的逆定理)命题:有四条边相等的四边形是菱形。已知:在四边形ABCD中,AB=BC=CD=DA.求证:四边形ABCD是菱形DABC证明:∵AB=CD,AD=BC∴四边形ABCD是平行四边形又∵AB=AD,∴四边形ABCD是菱形四条边都相等的四边形是菱形.AB=BC=CD=DAABCD菱形ABCD∵在四边形ABCD中AB=BC=CD=DA∴四边形ABCD是菱形四边形ABCDABCD判定方法3:数学语言老师说下列三个图形都是菱形,你相信吗?5534345555有一组邻边相等的平行四边形叫做菱形对角线互相垂直的平行四边形是菱形有四条边相等的四边形是菱形。3344┍活动三学以致用1.□ABCD的对角线AC与BD相交于点O,(1)若AB=AD,则□ABCD是形;(2)若AC=BD,则□ABCD是形;(3)若∠ABC是直角,则□ABCD是形;(4)若∠BAO=∠DAO,则□ABCD是形。ABCDO菱矩矩菱2、如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形。HGFEDCBA证明:连接AC、BD∵四边形ABCD是矩形∴AC=BD∵点E、F、G、H为各边中点1122EFGHBDFGEHAC,∴EF=FG=GH=HE∴四边形EFGH是菱形请你动脑筋把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?ACDB活动四:DCBAEF菱形常用的判定方法:①有一组邻边相等的平行四边形叫做菱形②对角线互相垂直的平行四边形是菱形③有四条边相等的四边形是菱形。+邻边相等=+对角线线互相垂直=四条边相等+=