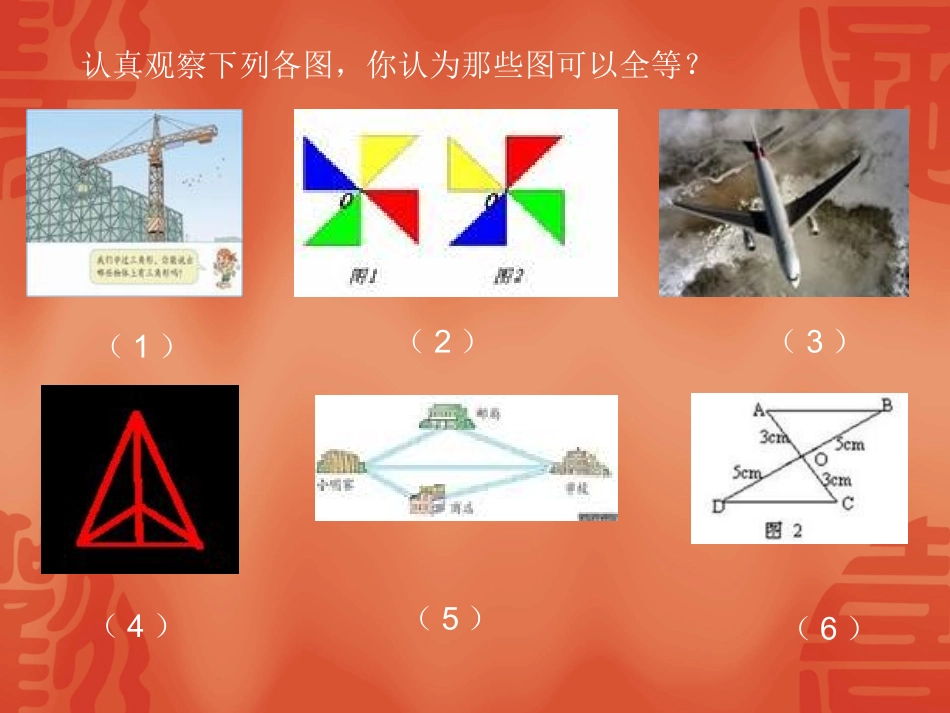
张胜方张胜方一、全等三角形有那些性质?(回顾)1:全等三角形的对应边相等;2:全等三角形的对应角相等。二、问题(想一想、做一做):我们从三角形的性质可知:三角形全等能够得出对应边、对应角分别相等.那么,如何判定两个三角形全等呢?即全等的条件是什么?(1)(2)(3)(4)(5)(6)认真观察下列各图,你认为那些图可以全等?在两个三角形中,如果有两边和它们的夹角对应相等,那么这两个三角形全等吗?BB'CAC'A'(C')(B')(A')ACB利用(平移)旋转、重合等加以说明!!旋转、重合三角形全等判定定理一:(边角边定理)有两边及它们的夹角对应相等的两个三角形全等(可简写成“边角边”或“SAS”)如图:用符号语言表达为:在△ABC与△A’B’C’中因为AB=A’B’∠B=B∠’BC=B’C’所以△ABCA’B’C’≌△BCAB'C'A'例1:在图3-34中,AB和CD相交于O,且AO=BO,CO=DO,试问△ACO和△BOD全等吗?OBDAC解:在△ACO和△BDO中,因为AO=BO(已知)∠AOC=BOD∠(对顶角相等)CO=DO(已知)所以△ACOBOD≌△(SAS).1、已知:AB=AC,AD=AE,∠2=1∠。证明:△ADBAEC≌△21ECBDA证明:因为∠2=1∠(已知)所以∠2+BAE=1+EAB∠∠∠从而∠CAE=BAD∠(等式的性质)又因为AB=AC(已知)∠BAD=CAE∠(已证)AD=AE(已知)所以△ADBAEC≌△例2在图3-36,正在修建的高速公路要通过一座大山,现要从这座山中挖一条隧道,为了预算修这条隧道的造价,必须知道隧道的长度,即这座山A,B两处的距离,你能想出一个办法,测出AB的长度吗?解选择一个合适的地点O,能够从O处看到隧道两端A、B处.连接AO并延长AO至A’,使OA’=OA;连接BO并延长BO至B’,使得,OB’=OB.连接A’B’.在△AOB和△A’OB’中,因为AO=A’O∠AOB=A’OB’(∠对顶角相等)BO=B’O所以△AOBA’OB’(SAS)≌△故A’B’=AB()因此A’B’的长度就是这座大山A处与B处所求的距离B'A'ABOB'A'ABO分离图七、小结:说一说同学们你们这节课学到了什么,把你所学到的知识说出来与大家分享一下,好吗?三角形全等的条件:1、有两边和它们的夹角对应相等的两个三角形全等(SAS);2、用SAS判定三角形全等的注意点(1)至少三个条件(2)必须是两边一夹角。若不是夹角,不一定全等(3)全等的三个条件必须是三角形的对应边和对应角。若条件不完全,则必须先证明三个条件八、作业P75练习1、2补充:如下左图所示,AC=AD,AE=AB,证明:BC=ED.思考题如图,△ABODCO≌△,且BO=CO,试说明△ABCDCB≌△?ODABC思考题EDACB