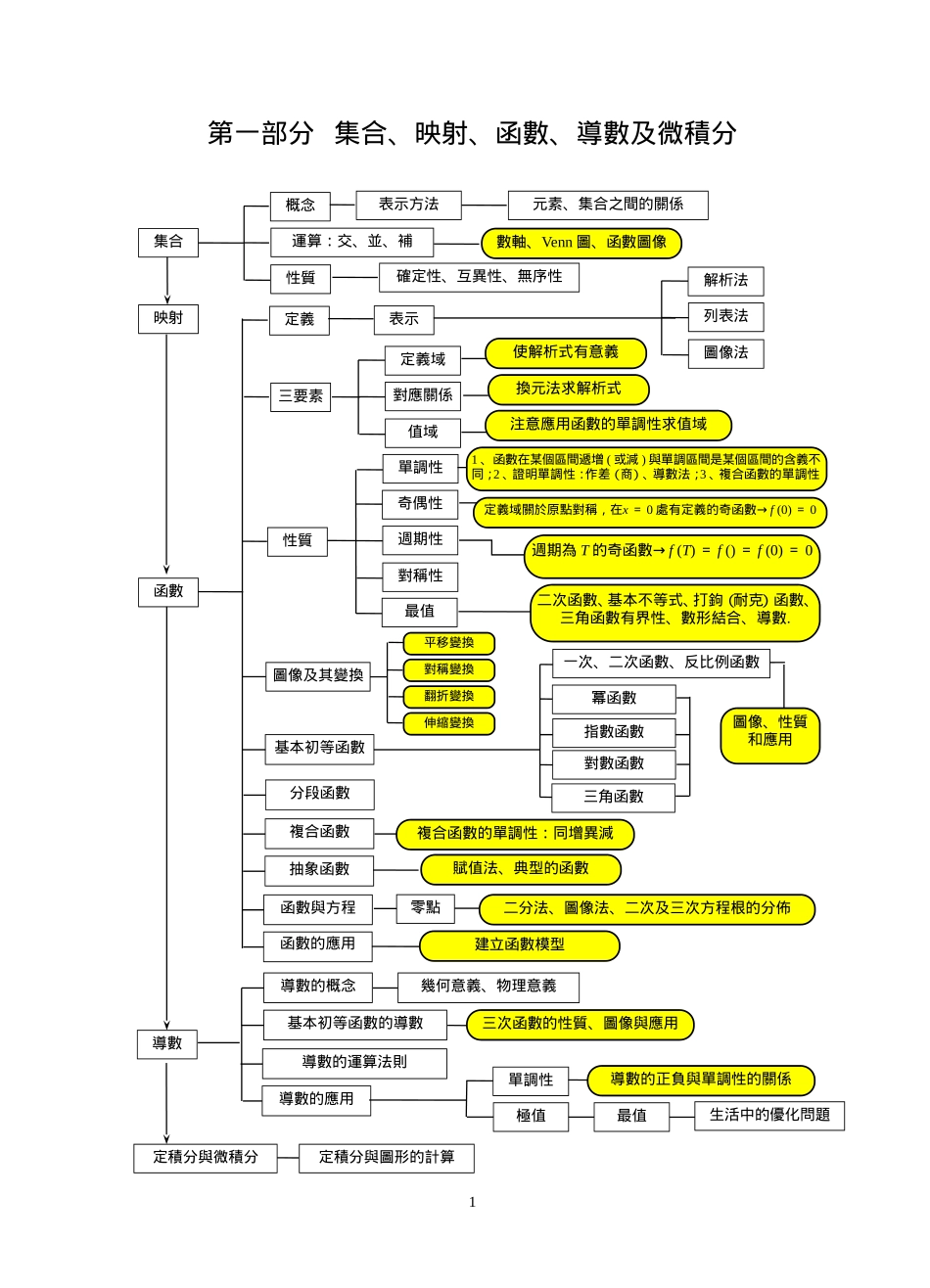
第一部分集合、映射、函數、導數及微積分1集合映射概念元素、集合之間的關係運算:交、並、補數軸、Venn圖、函數圖像性質確定性、互異性、無序性定義表示解析法列表法三要素圖像法定義域對應關係值域性質奇偶性週期性對稱性單調性定義域關於原點對稱,在x=0處有定義的奇函數→f(0)=01、函數在某個區間遞增(或減)與單調區間是某個區間的含義不同;2、證明單調性:作差(商)、導數法;3、複合函數的單調性最值二次函數、基本不等式、打鉤(耐克)函數、三角函數有界性、數形結合、導數.冪函數對數函數三角函數基本初等函數抽象函數複合函數賦值法、典型的函數函數與方程二分法、圖像法、二次及三次方程根的分佈零點函數的應用建立函數模型使解析式有意義導數函數基本初等函數的導數導數的概念導數的運算法則導數的應用表示方法換元法求解析式分段函數幾何意義、物理意義單調性導數的正負與單調性的關係生活中的優化問題定積分與微積分定積分與圖形的計算注意應用函數的單調性求值域週期為T的奇函數→f(T)=f()=f(0)=0複合函數的單調性:同增異減三次函數的性質、圖像與應用一次、二次函數、反比例函數指數函數圖像、性質和應用平移變換對稱變換翻折變換伸縮變換圖像及其變換最值極值第二部分三角函數與平面向量2角的概念任意角的三角函數的定義同角三角函數的關係三角函數弧度制弧長公式、扇形面積公式三角函數線同角三角函數的關係誘導公式和角、差角公式二倍角公式“公式的變形、逆用、1”的替換化簡、求值、證明(恒等變形)三角函數的圖象定義域奇偶性單調性週期性最值對稱軸(正切函數除外)經過函數圖像的最高(或低)點且垂直x軸的直線,對稱中心是正余弦函數圖像的零點,正切函數的對稱中心為(,0)(k∈Z).正弦函數y=sinx=余弦函數y=cosx正切函數y=tanxy=Asin(x+)+b①圖像可由正弦曲線經過平移、伸縮得到,但要注意先平移後伸縮與先伸縮後平移不同;②圖像也可以用五點作圖法;③用整體代換求單調區間(注意的符號);④最小正週期T=;⑤對稱軸x=,對稱中心為(,b)(k∈Z).平面向量概念線性運算基本定理加、減、數乘幾何意義座標表示數量積幾何意義模共線與垂直共線(平行)垂直值域圖像∥=x1y2-x2y1=0⊥·=0x1x2+y1y2=0解三角形余弦定理面積正弦定理解的個數的討論實際應用S△=ah=absinC=(其中p=)投影在方向上的投影為||cos=設與夾角,則cos=對稱性||=夾角公式第三部分數列與不等式3概念數列表示等差數列與等比數列的類比解析法:an=f(n)通項公式圖像法列表法遞推公式等差數列通項公式求和公式性質判斷an=a1+(n-1)dan=a1qn-1an+am=ap+aranam=apar前n項和Sn=前n項積(an>0)Tn=常見遞推類型及方法逐差累加法逐商累積法構造等比數列{an+}構造等差數列①an+1-an=f(n)②=f(n)③an+1=pan+q④pan+1an=an-an+1化為=·+1轉為③⑤an+1=pan+qn等比數列an≠0,q≠0Sn=公式法:應用等差、等比數列的前n項和公式分組求和法倒序相加法裂項求和法錯位相加法常見求和方法不等式不等式的性質一元二次不等式簡單的線性規劃基本不等式:≤數列是特殊的函數借助二次函數的圖像三個二次的關係可行域目標函數一次函數:z=ax+byz=:構造斜率z=:構造距離應用題幾何意義:z是直線ax+by-z=0在x軸截距的a倍,y軸上截距的b倍.最值問題變形和定值,積最大;積定值,和最小應用時注意:一正二定三相等≤≤≤第四部分解析幾何4傾斜角和斜率直線的方程位置關係直線方程的形式傾斜角的變化與斜率的變化重合平行相交垂直A1B2-A2B1=0A1B2-A2B1≠0A1A2+B1B2=0點斜式:y-y0=k(x-x0)斜截式:y=kx+b兩點式:=截距式:+=1一般式:Ax+By+C=0注意各種形式的轉化和運用範圍.兩直線的交點距離點到線的距離:d=,平行線間距離:d=圓的方程圓的標準方程圓的一般方程直線與圓的位置關係兩圓的位置關係相離相切相交<0,或d>r=0,或d=r>0,或d<r曲線與方程軌跡方程的求法:直接法、定義法、相關點法圓錐曲線橢圓雙曲線抛物線定義及標準方程性質範圍、對稱性、頂點、焦點、長軸(實軸)、短軸(虛軸)、...