高中数学 两条直线平行与垂直的判定课件 新人教A版必修2 课件VIP免费

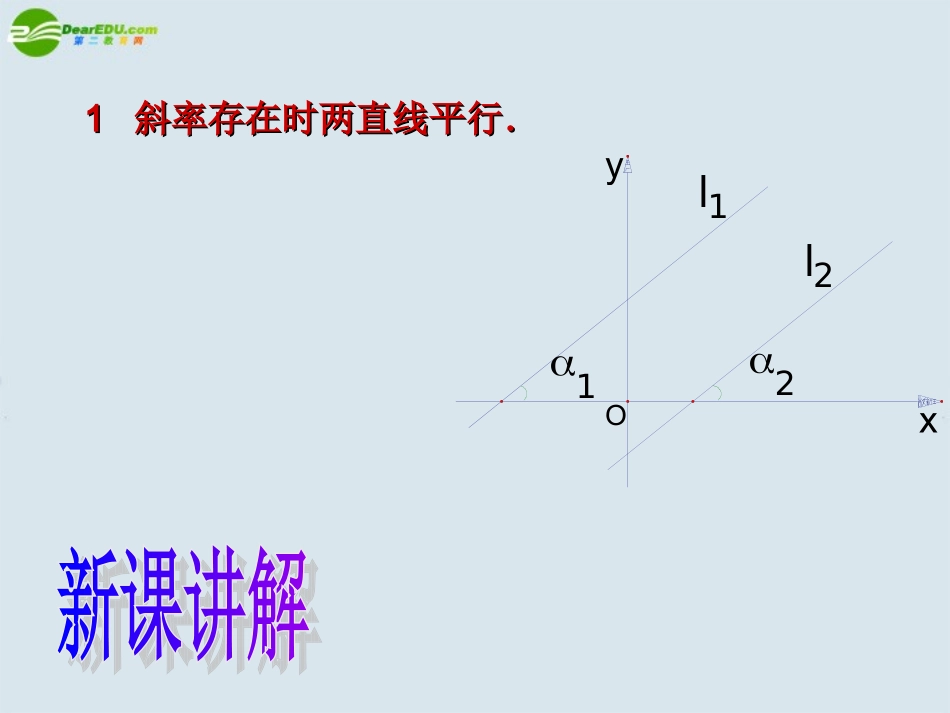
11斜率存在时两直线平行．斜率存在时两直线平行．l2l121xOy结论结论1:1:如果直线L1,L2的斜率为k1,k2.那么L1∥L2k1=k2注意注意::上面的等价是在两直线斜率存在的前提下才成立的，上面的等价是在两直线斜率存在的前提下才成立的，缺少这个前提，结论并不存立．缺少这个前提，结论并不存立．特殊情况下的两直线平行特殊情况下的两直线平行::两直线的倾斜角都为两直线的倾斜角都为90°90°，互相平行，互相平行..例题讲解例题讲解例例11例例22例例3:3:求与直线求与直线2x+3y+5=02x+3y+5=0平行，且在两坐标轴上的截距之平行，且在两坐标轴上的截距之和为的直线的方程．和为的直线的方程．65一般地，直线一般地，直线Ax+By+C=0Ax+By+C=0中系数中系数AA、、BB确定直线的斜率，确定直线的斜率，因此，与直线因此，与直线Ax+By+C=0Ax+By+C=0平行的直线方程可设为平行的直线方程可设为Ax+By+Ax+By+=0=0，，其中其中待定待定（直线系）（直线系）11若直线和平行，则若直线和平行，则==。。a12ayx122ayx0022若直线和平行，则若直线和平行，则==。。a1ayax22aayx11046Cyx012yAx33直线和直线平行直线和直线平行的条件是的条件是。。22斜率存在时两直线垂直．斜率存在时两直线垂直．甲l2l121xOy乙l2l121xOy丙l2l121xOy结论结论22：：如果两直线的斜率为k1,k2,那么,这两条直线垂直的充要条件是k1·k2=-1注意注意::上面的等价是在两直线斜率存在的前提下才成立的，上面的等价是在两直线斜率存在的前提下才成立的，缺少这个前提，结论并不存立．缺少这个前提，结论并不存立．0,1212121为一斜率不存在另一斜率或llkkll特殊情况下的两直线平行与垂直．特殊情况下的两直线平行与垂直．当两条直线中有一条直线没有斜率时：当两条直线中有一条直线没有斜率时：当另一条直线的斜率为当另一条直线的斜率为00时，时，则一条直线的倾斜角为则一条直线的倾斜角为909000,,另一条直线的倾斜角为另一条直线的倾斜角为0°0°两直线互相垂直两直线互相垂直例例44已知直线与已知直线与互相垂直，求互相垂直，求的值的值02)32()1(yaxa03)1()2(yaxa例例5:5:求过点求过点A(2,1)A(2,1)且与直线且与直线2x+y-10=02x+y-10=0垂直的直线的方程垂直的直线的方程注意：注意：①①解法一求直线方程的方法是通法，必须掌握；解法一求直线方程的方法是通法，必须掌握；②②解法二是常常采用的解题技巧：解法二是常常采用的解题技巧：一般地，由于与直线一般地，由于与直线Ax+By+C=0Ax+By+C=0垂直的直线的斜率互为负垂直的直线的斜率互为负倒数，故可得其方程为倒数，故可得其方程为Bx-Ay+Bx-Ay+=0=0，，其中其中待定待定（直线系）（直线系）22如果直线L1,L2的方程为L1:A1x+B1y+C1=0,L2:A2x+B2y+C2=0(A1B1C1≠0,A2B２C２≠0)那么L1⊥L2的充要条件是A1A2+B1B2=111如果直线L1,L2的方程为L1:A1x+B1y+C1=0,L2:A2x+B2y+C2=0(A1B1C1≠0,A2B２C２≠0)那么L1∥L2的充要条件是212121CCBBAA如果直线L1,L2的斜截式方程为L1:y=k1x+b1,L2:y=k2x+b2,那么L1L2∥k1=k2且b1≠b2斜率都不存在且不重合或且21212121,//llbbkkll例例11：：两条直线两条直线LL11:2x-4y+7=0:2x-4y+7=0，，LL22:x-2y+5=0:x-2y+5=0求证求证:L:L11∥L∥L22例例22：：求过点求过点A(1,-4)A(1,-4)且与直线且与直线2x+3y+5=02x+3y+5=0平行的直线的方程。平行的直线的方程。注意：注意：①①解法一求直线方程的方法是通法，必须掌握；解法一求直线方程的方法是通法，必须掌握；②②解法二是常常采用的解题技巧。解法二是常常采用的解题技巧。