高中数学 117 柱、锥、台和球体的体积 课件 新人教B版必修2 课件VIP免费

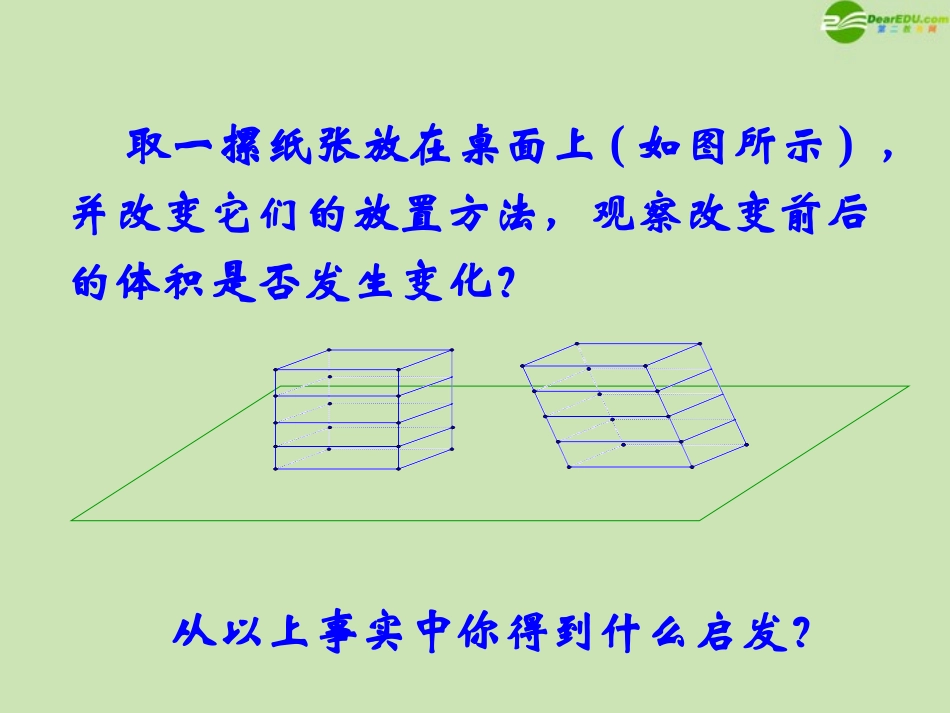
1.1.7柱、锥、台和球体的体积取一摞纸张放在桌面上(如图所示)，并改变它们的放置方法，观察改变前后的体积是否发生变化？从以上事实中你得到什么启发？一.祖暅原理祖暅原理：幂势既同，则积不容异.也就是说，夹在两个平行平面间的两个几何体，被平行于这两个平面的任意平面所截，如果截得的两个截面的面积总相等，那么这两个几何体的体积相等.祖原理是推导柱、锥、台和球体积暅公式的基础和纽带，原理中含有三个条件，条件一是两个几何体夹在两个平行平面之间；条件二是用平行于两个平行平面的任何一平面可截得两个平面；条件三是两个截面的面积总相等，这三个条件缺一不可，否则结论不成立.二.棱柱和圆柱的体积柱体（棱柱和圆柱）的体积等于它的底面积S和高h的积.即V柱体=S·h.hh底面半径是R，高为的圆柱体的体积的计算公式是S圆柱=πR2h.三.棱锥和圆锥的体积1.如果一个锥体（棱锥、圆锥）的底面积是S，高是h，那么它的体积是V锥体=Sh.312.如果圆锥的底面半径是R，高是h，则它的体积是V圆锥=πR2h.31B'C'A'CBAA'BCA'ABCA'B'C'C'B'PS'hSO'OD'DABCA'B'C'四.棱台和圆台的体积1.V台体=；其中S、S’分别为台体上、下底面面积，h为台体的高.1('')3SSSSh2．V圆台=π(r2+Rr+R2)h,其中r、R分别为圆台的上、下底面的半径，高为h.S'Sxhsshxx'''ssshxxSxhSV'31)31（台xSSxSh'313131''')(3131ssshSSSh'')(3131shssSh)(31''ssssh五.球的体积V球=，其中R为球的半径.343R柱体、锥体、台体的体积公式间的关系例1.如图所示，在长方体ABCD－A’B’C’D’中，用截面截下一个棱锥C－A’DD’，求棱锥C－A’DD’的体积与剩余部分的体积之比。D'DABCA'B'C'解：已知长方体可以看作是直四棱柱ADD’A’－BCC’B’。设底面ADD’A’的面积是S，高为h，则它的体积为V=Sh.因为棱锥C－A’DD’的底面面积是S，高是h，12所以棱锥C－A’DD’的体积是VC－A’DD’=111326ShSh所以棱锥C－A’DD’的体积与剩余部分的体积之比是1：5.例2．有一堆规格相同的铁制(铁的密度是7.8g/cm3)六角螺帽共重5.8kg，已知螺帽底面是正六边形，边长为12mm,内孔直径为10mm，高为10mm，问这堆螺帽大约有多少个（取3.14，可用计算器）？解：六角螺帽的体积是六棱柱的体积与圆柱体积之差，10)210(14.3106124322V)(29563mm)(956.23cm因此约有5.8×103÷(7.8×2.956)≈252(个)答：螺帽的个数约为252个.练习题：1．设六正棱锥的底面边长为1，侧棱长为，那么它的体积为（）（A）6（B）（C）2（D）25333B2．正棱锥的高和底面边长都缩小原来的，则它的体积是原来的（）（A）（B）（C）（D）211518116132B3．直三棱柱ABC－A1B1C1的体积为V，已知点P、Q分别为AA1、CC1上的点，而且满足AP=C1Q，则四棱锥B－APQC的体积是（）（A）（B）（C）（D）12V13V14V23VB4．把一个大金属球表面涂漆，需油漆2.4kg，若把这个金属球熔化，制成64个半径相等的小金属球（设损耗为零），将这些小金属球表面涂漆，需用油漆kg.9.65．已知圆锥的母线长为8，底面周长为6π，则它的体积是.3556．一个正方体的所有顶点都在球面上，若这个球的体积是V，则这个正方体的体积是.233V7.若球的大圆面积扩大为原来的3倍，则它的体积扩大为原来的（）（A）3倍（B）9倍（C）27倍（D）3倍3D8.圆台的上、下底面半径和高的比为1：4：4，母线长10，则圆台的体积为（）（A）672π（B）224π（C）100π（D）5443B