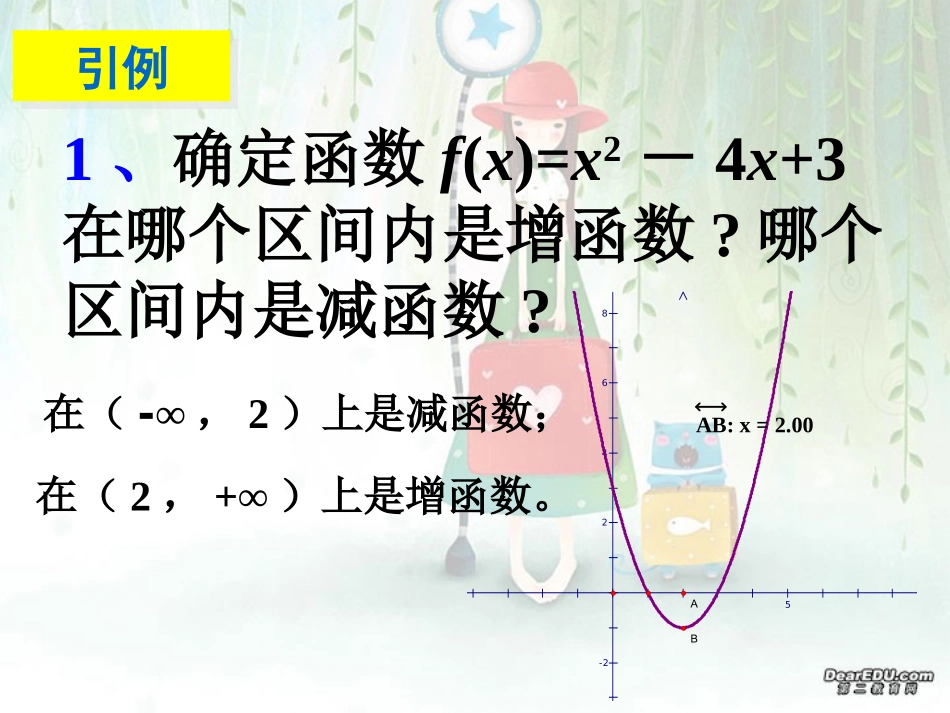
导数的应用用导数研究函数的单调性1、确定函数f(x)=x2-4x+3在哪个区间内是增函数?哪个区间内是减函数?引例引例8642-2-4-6-8-10-5510AB:x=2.00fx=x2-4x+3AB在(-∞,2)上是减函数;在(2,+∞)上是增函数。2、确定函数f(x)=2x3-6x2+7在哪个区间内是增函数?哪个区间内是减函数?引例引例用定义法判断函数单调性的步骤:(1)在给定的区间内任取x10)>0,,则则ff((xx))为这个区间内的增函数为这个区间内的增函数;;如果在这个区间内如果在这个区间内ff′′((xx)<)<0,0,则则ff((xx))为这个区间内的减函数为这个区间内的减函数..注意注意::如果在如果在某个区间内恒有某个区间内恒有ff′(′(xx))=0=0,,则则ff((xx))为为常数函数常数函数。。判断方法判断方法研究数学问题的一般方法:研究数学问题的一般方法:从特殊到一般;从简单到复杂。从特殊到一般;从简单到复杂。结论应用结论应用:由以上结论可知,函数的:由以上结论可知,函数的单调性与其导数有关,因此今后我们单调性与其导数有关,因此今后我们可以利用导数法去探讨函数的单调性可以利用导数法去探讨函数的单调性下面举例说明:下面举例说明:例题讲解例题讲解解题步骤解题步骤::11、求函数的导函数;、求函数的导函数;22:判断导函数在指定区间上的符号;:判断导函数在指定区间上的符号;33、下结论。、下结论。例1、求证:函数y=x3+1在上是增函数。(,0)根据导数确定函数的单调性一般需三步:根据导数确定函数的单调性一般需三步:1.1.确定函数确定函数ff((xx))的定义域的定义域;;2.2.求出函数的导数;求出函数的导数;3.3.解不等式解不等式ff′′((xx)>)>0,0,得函数单增区间得函数单增区间;;解不等式解不等式ff′(′(xx)<)<0,0,得函数单减区间。得函数单减区间。例2、确定函数f(x)=2x3-6x2+7在哪个区间内是增函数?哪个区间内是减函数?课堂练习课堂练习1、确定下列函数的单调区间。yxxx32(1)924;3(2)3.yxx单调增区间为:(4,+∞)和(-∞,2)单调减区间为:(2,4)单调增区间为:(-1,1)单调减区间为:(-∞,-1)和(1,+∞)课堂练习课堂练习2,设f/(x)是函数f(x)的导函数,y=/(x)的图象如左图所示,则y=(x)的图象最有可能的是()xyO12(B)xyO12(A)xyO12yx12(C)OOxyO12(D)C1.函数导数与单调性的关系:若函数y=f(x)在某个区间内可导,如果f′(x)>0,则f(x)为增函数;如果f′(x)<0,则f(x)为减函数。2.本节课中,用导数去研究函数的单调性是中心,能灵活应用导数解题是目的,另外应注意数形结合在解题中应用。3.掌握研究数学问题的一般方法:从特殊到一般;从简单到复杂。课堂总结课堂总结1:能不能画出该函数的草图?2:32276(0,2)xx在有几解?思考题思考题函数f(x)=2x3-6x2+7作业布置作业布置课堂作业:课本p42习题2.41,2课外作业:完成《数学之友》相关内容