高一数学(向量数乘运算)课件VIP免费

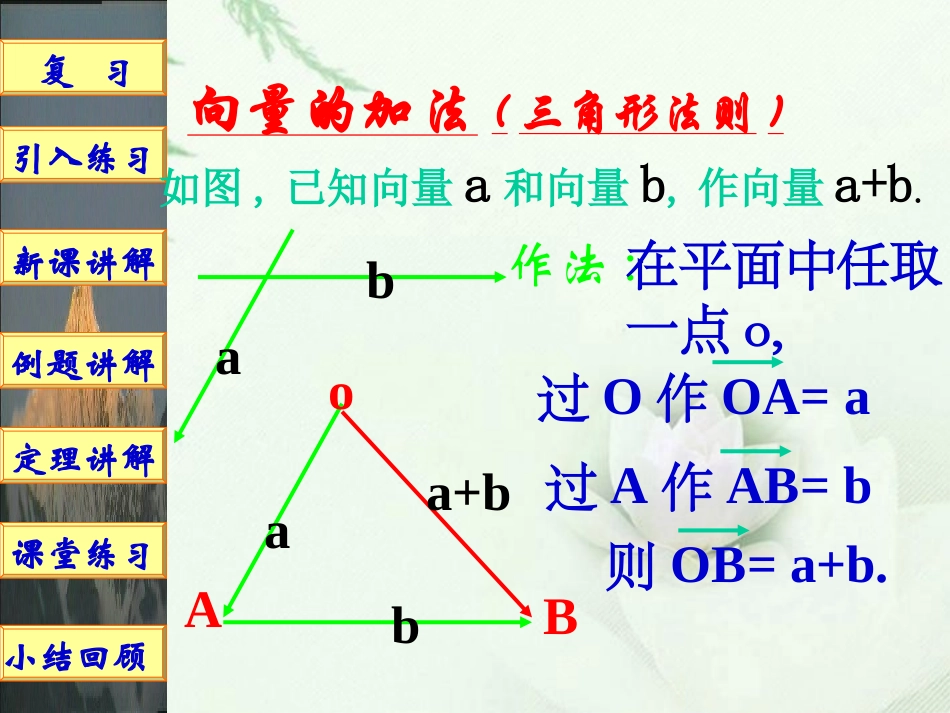
向量的加法(三角形法则)如图,已知向量a和向量b,作向量a+b.ab作法:在平面中任取一点o,aAbBa+b过O作OA=a则OB=a+b.过A作AB=bo复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习向量的加法(平行四边形法则)如图,已知向量a和向量b,作向量a+b.a作法:在平面中任取一点o,过O作OA=a过O作OB=boaAbBb以OA,OB为边作平行四边形则对角线OC=a+ba+bC复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习向量的减法(三角形法则）如图,已知向量a和向量b,作向量a-b.ab作法:在平面中任取一点o,过O作OA=a过O作OB=boaAbB则BA=a-ba-b复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习试作出：试作出：aa++aa++aa和和(-(-aa)+(-)+(-aa)+(-)+(-aa))已知非零向量已知非零向量aa（如图）（如图）aaaaaaaaOOAABBCC-a-a-a-a-a-aPPQQMMNN相同向量相加以后，相同向量相加以后，和的长度与方向有什么变化？和的长度与方向有什么变化？复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习一般地，实数一般地，实数λλ与向量与向量aa的的积积是一个是一个向量向量，，这种运算叫做这种运算叫做向量的数乘运算向量的数乘运算，记作，记作λλaa，，它的它的长度长度和和方向方向规定如下：规定如下：(1)|(1)|λλaa|=||=|λλ||||aa||(2)(2)当当λ>0λ>0时时,,λλaa的方向与的方向与aa方向相同；方向相同；当当λ<0λ<0时时,,λλaa的方向与的方向与aa方向相反；方向相反；特别地，当特别地，当λ=0λ=0或或a=0a=0时时,,λλaa==00复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习(1)(1)根据定义，求作向量根据定义，求作向量3(23(2aa))和和(6(6aa))((aa为非零向量为非零向量))，并进行比较。，并进行比较。(2)(2)已知向量已知向量a,ba,b，求作向量，求作向量2(2(a+ba+b))和和22a+a+22bb，并进行比较。，并进行比较。复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习a)2(3a)2(3aa6=abbaba22a2b2baba22)(2设设a,ba,b为任意向量，为任意向量，λ,μλ,μ为任意为任意实数实数，则有：，则有：①①λ(μλ(μaa)=(λμ))=(λμ)aa②②((λ+μλ+μ))a=a=λλa+a+μμaa③③λ(λ(a+ba+b)=λ)=λa+a+λλbb例例11计算：计算：(1)((1)(--3)×43)×4aa(2)3((2)3(a+ba+b))–2(–2(a-ba-b))-a-a(3)(2(3)(2aa+3+3b-cb-c))–(3–(3a-a-22bb++cc))-1-122aa55bb-a+-a+55b-b-22cc复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习ab,、向量的加、减、数乘运算统称为向量的线性运算。对于任意的向量以及任意实数恒有12、、，22aa11(b)=b对于向量对于向量a(a≠0),ba(a≠0),b，以及实数，以及实数λ,μλ,μ问题问题11：如果：如果b=b=λλa,a,那么，向量那么，向量aa与与bb是否共是否共线？线？问题问题22：如果：如果向量向量aa与与bb共线共线那么，那么，b=b=λλaa？？向量向量bb与非零向量与非零向量aa共线共线当且仅当当且仅当有唯一有唯一一一个实数个实数λλ，使得，使得b=b=λλaa复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习例例22如图，已知如图，已知AD=3ABAD=3AB，，DE=3BDE=3BCC，，试判断试判断ACAC与与AEAE是否共线。是否共线。ADECB复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习向量向量bb与非零向量与非零向量aa共线共线当且仅当当且仅当有且只有一个实数有且只有一个实数λλ，使得，使得b=b=λλaa小结回顾小结回顾一、一、①①λλaa的定义及运算律的定义及运算律②②向量共线定理向量共线定理(a≠0)(a≠0)b=b=λλaa向量向量aa与与bb共线共线二、定理的应用：二、定理的应用：1.1.证明向量共线证明向量共线2.2.证明三点共线证明三点共线:AB=:AB=λλBCA,B,CBCA,B,C三点共线三点共线3.3.证明两直线平行证明两直线平行::AB=AB=λλCDABCD∥CDABCD∥ABAB与与CDCD不在同一直线上不在同一直线上直线直线AB∥AB∥直线直线CDCD作业：P102，12.13课本课本::PP101101第第99题（题（33））（（44））PP102102第第44题题复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习如图，在平行四边形如图，在平行四边形ABCDABCD中，点中，点MM是是ABAB中点，中点，点点NN在线段在线段BDBD上，且有上，且有BN=BDBN=BD，求证：，求证：MM、、NN、、CC三点共线。三点共线。31ADBCMN复习例题讲解小结回顾引入练习新课讲解定理讲解课堂练习提示：设提示：设AB=AB=aaBC=BC=bb则则MN=…=MN=…=a+a+bb6131MC=…=MC=…=a+a+bb21