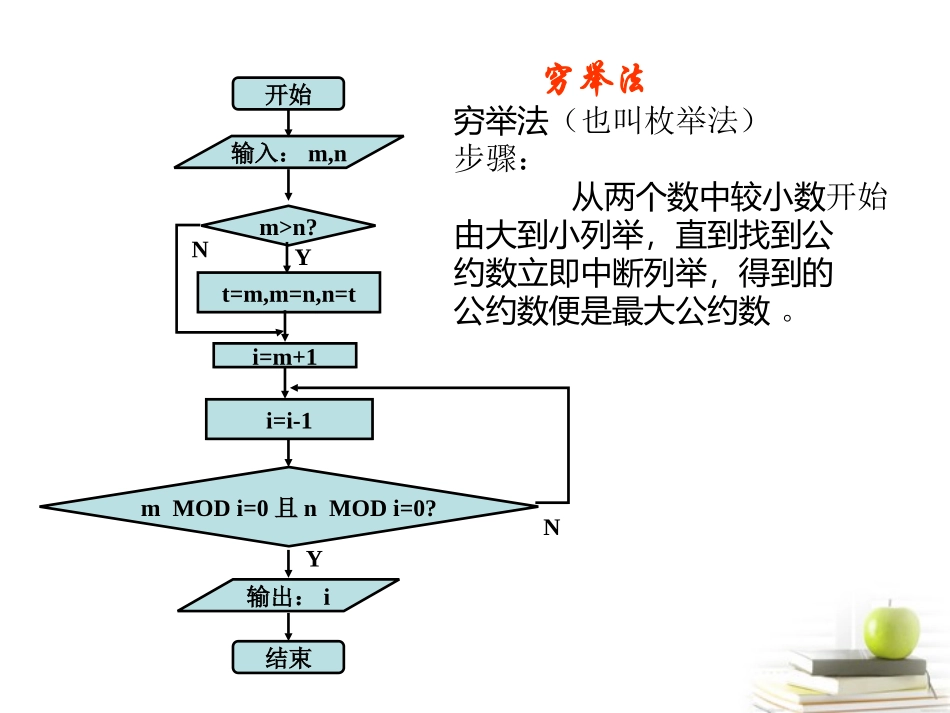
一位美国的幼儿园老师为了教育孩子火海逃生,引导学生做了一个非非常有趣的游戏──“火海逃生”。老师将许多乒乓球放进瓶子,只露出系着的棉线。花瓶代表大楼,细细的瓶颈是惟一的出口,七只乒乓球则是楼里的居民,要求当大楼突然起火时,全体居民能在短时间里安全逃离。七名学生兴奋地上场了,他们各执一根棉线,报警器一响,都以最快的反应拉扯绳子,可一个“人”也没能脱离火海,原来,七只乒乓球都卡在了瓶口。又开始了第二次实验?这几个学生面面相觑,只见其中一个小声跟同伴们商量了几句,这回大家没有各顾各地拉绳子,而是由左到右依次地拉。果然,报警器的尾音还没结束,七位“居民”已离开了出口,转移到了安全地带。运筹帷幄,决胜千里算法案例之求最大公约数求以下几组正整数的最大公约数。(注:若整数m和n满足n整除m,则(m,n)=n。用(m,n)来表示m和n的最大公约数。)(1)(18,30)(2)(24,16)(3)(63,63)(4)(72,8)(5)(301,133)解:21824用公有质因数2除,3912用公有质因数3除,343和4互质不除了。得:18和24最大公约数是:2×3=6想一想,如何求8251与6105的最大公约数?例、求18与24的最大公约数:6;8;63;8;7;短除法开始i=m+1输入:m,nmMODi=0且nMODi=0?i=i-1输出:i结束YNm>n?t=m,m=n,n=tNY穷举法(也叫枚举法)步骤:从两个数中较小数开始由大到小列举,直到找到公约数立即中断列举,得到的公约数便是最大公约数。穷举法定理:已知m,n,r为正整数,若m=nq+r(0≤r