高三数学高考冲刺模拟课件人教大纲版 课件VIP免费

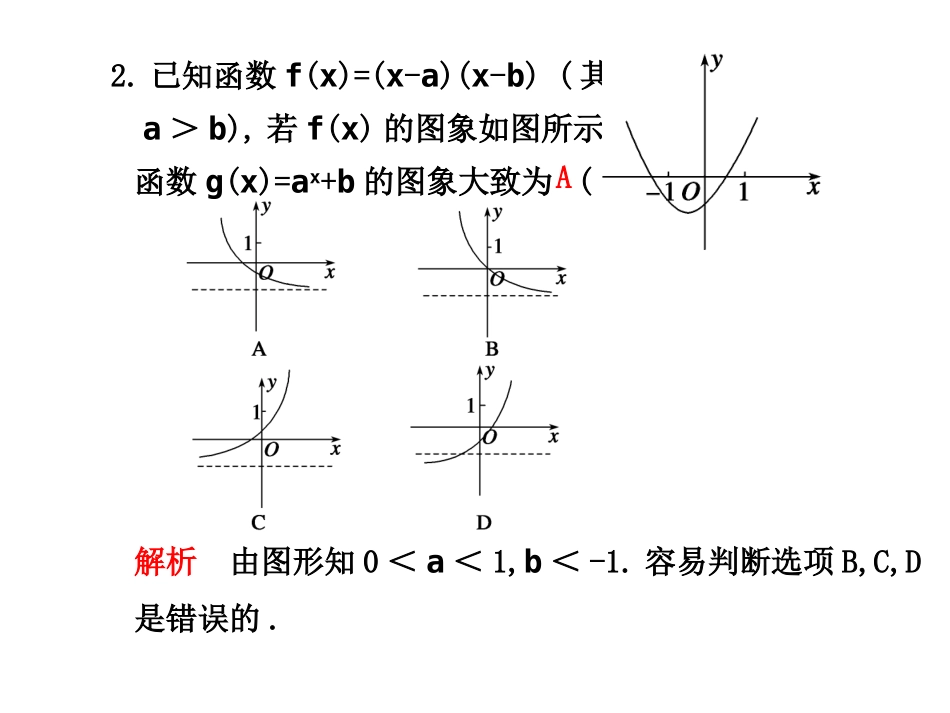
一、选择题(每小题5分,共60分)1.设f:x→x2是集合A到集合B的映射,如果B={1,2},则A∩B等于()A.{1}B.C.或{1}D.或{2}解析由已知可得集合A是集合{,-1,1,}的非空子集,则A∩B=或{1}.高考冲刺模拟C222.已知函数f(x)=(x-a)(x-b)(其中a＞b),若f(x)的图象如图所示,则函数g(x)=ax+b的图象大致为()解析由图形知0＜a＜1,b＜-1.容易判断选项B,C,D是错误的.A3.函数f(x)=3sin(x+20°)+5sin(x+80°)的最大值为()A.6B.C.7D.8解析因为f(x)=3sin(x+20°)+5sin(x+80°),令t=x+20°,原式可化为:g(t)=3sint+5sin(t+60°)=所以(g(t))max=7,即(f(x))max=7.),sin(7cos235sin211tttC2134.函数f(x)=log3x的定义域为M=[1,9],若函数g(x)=[f(x)]2+f(x2)的定义域为N.则下面四个命题:①M=N;②MN;③M∩N=N;④M∪N=N中,真命题的个数为()A.1B.2C.3D.4解析由题意可知:g(x)=[f(x)]2+f(x2)的定义域为即N=[1,3],又M=[1,9],所以NM,即M∩N=N.,3191912xxxA5.若函数f(x)=x3+f′(1)x2-f′(2)x+3,则f(x)在点(0,f(0))处切线的倾斜角为()A.B.C.D.解析由题意可知f′(x)=x2+f′(1)x-f′(2),令x=0,得f′(0)=-f′(2),令x=1,得f′(2)=1,所以f′(0)=-1,即433243.43D31216.直角坐标系xOy中,i,j分别是与x,y轴正方向同向的单位向量,在直角三角形ABC中,若=2i+j,=3i+kj,则k的可能值个数是()A.1B.2C.3D.4解析=-2i-j+3i+kj=i+(k-1)j.(1)若A为直角,则=(2i+j)(3i+kj)=6+k=0k=-6;(2)若B为直角,则=(2i+j)[i+(k-1)j]=1+k=0k=-1;ABACACBABCACABBCAB(3)若C为直角,则=(3i+kj)[i+(k-1)j]=k2-k+3=0k∈.所以k的可能值个数是2.答案B7.已知(n∈N*),则数列{an}的最小值为()A.6B.7C.8D.解析设有1≤t≤3,则用导数可以证明,函数在1≤t≤3上是递减的,所以当t=3时,an取最小值BCAC6sin2166sinnnan.319319,6sin2nt.216ttantttf16)(D8.在正四面体S—ABC中,E为SA的中点,F为△ABC的中心,则异面直线EF与AB所成的角是()A.30°B.45°C.60°D.90°解析过F作FM∥AB交AC于点M,连接EM,EF,SF,AF,则∠EFM是异面直线AB、EF所成的角或其补角,因为点F是底面的中心,∴AF平分∠BAC,又FM∥AB,∴AM=FM, SF⊥面ABC,∴SF⊥AF, E是SA的中点,∴AE=FE,又EM为公共边,∴△MAE≌△MFE,∴∠MAE=∠MFE,∴∠EFM=60°.C9.从编号为1，2，…，10的10个大小相同的球中任取4个，则所取4个球的最大号码是6的概率为()A.B.C.D.解析从10个球中任选4个共有种取法，所取4个球中最大号码是6的取法共有种，所求概率为8412115253B410C35C.21141035CCp10.已知实数x、y满足则的取值范围是()A.B.C.D.解析若设P(x,y),A(1,2),B(4,6),由题意可知:|PA|-|PB|=5,而|AB|=5,即|PA|-|PB|=|AB|,因此点P在线段AB的延长线上,而表示点Q(-4,2)与点P(x,y)连线的斜率kPQ,由于kQB=kAB=由图象可知,5)6()4(22yx22)2()1(yx42xy42xy]34,21[)34,21[)31,21(),21[,21,34).34,21[42xykPQB11.已知函数f(x)=(x∈R)其图象如图所示,则实数a,b之间的数量关系为()A.a=2bB.a＞2bC.2a＞bD.2a＜b解析由题意结合图象可知a＞0,b＞0,所以在x=处,函数f(x)取到最大值,有图象可知x=＜1,所以0＜a＜1,＞2a.axbx2,)())(()()()('22222axxaxabaxxabxf又aaabaabaf2,12)(即又D12.已知定义在R上的函数f(x)满足:f(0)=0,f(x)+f(1-x)=1,且当0≤x1＜x2≤1时,总有f(x1)≤f(x2)成立,则等于()A.B.C.D.解析由f(0)=0,f(x)+f(1-x)=1,令x=0得f(1)=1;),(21)5(xfxf)1001(f214181161.81)41(21)201(21)1001(,21)41(,21)21()41()51(21;21)1(21)51(1),(21)5(,21)21(212fffffffffxxfxffx所以即所以得令又得令C二、填空题(每小题4分,共16分)13.已知a为直线x+2y+1=0的一个方向向量,b=(2,k),且a⊥b,则使不等式恒成立的实数m的取值范围为__________.解析由题意知,向量a=(1,),又b=(2,k)且a⊥b,所以即k=4,则|x-4|+|x-6|＞m2-3m-2,由绝对值(|x-4|+|x-6|)的几何意义可知：|x-4|+|x-6|≥2,所以2＞m2-3m-2,即-1＜m＜4.23|23|||2mmxkkx21,0),2()21,1(k(...