高中数学 各种类型不等式的基本解法课件 苏教版必修5 课件VIP免费

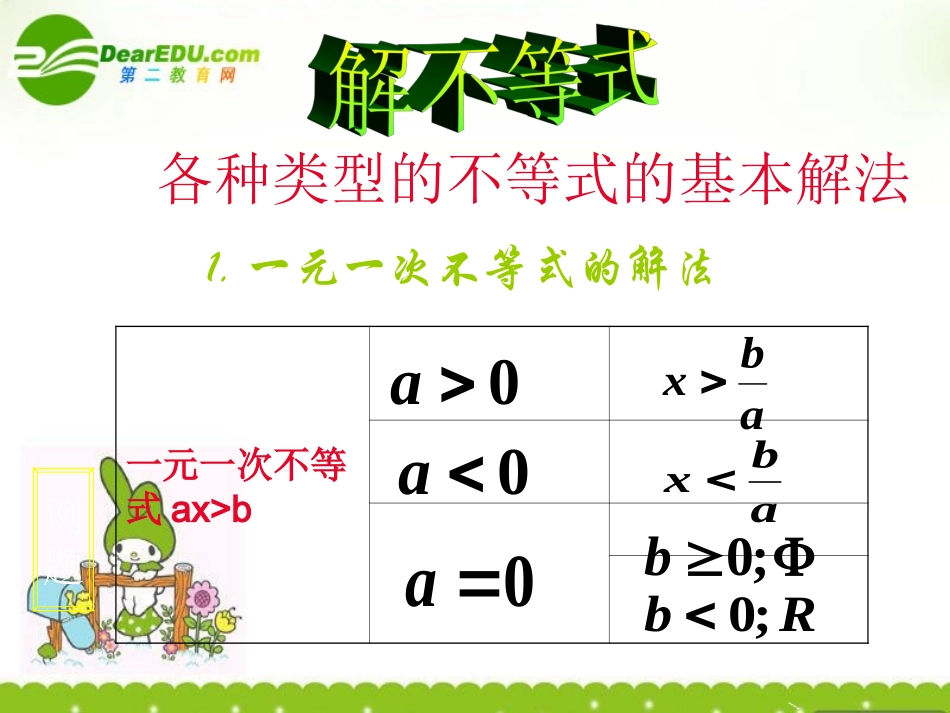
1.一元一次不等式的解法各种类型的不等式的基本解法一元一次不等式ax>babxabx0a0a0a;0bRb;0例题2.2.一元二次不等式的解法一元二次不等式的解法各种类型的不等式的基本解法各种类型的不等式的基本解法(注意几个问题)(1).化归为标准形式：(a>0))0(02或cbxax(2).因式分解：尤其是含字母的式子，如果能分解，则不必再用求根公式，同时也说明△恒正。如:x2-3(a+1)x+2(3a+1)=(x-2)[x-(3a+1)]要解不等式，只要讨论2与3a+1大小即可(3).注意对含参的二次项系数的讨论例题•对不等式进行等价转化，因式分解，达到：3.高次与分式不等式的解法(1).不等式的各个因式的系数必须为正如不能确定，则首先讨论系数的取值。(2).对各因式对应根进行排序，这也是引发讨论的一个重要因素。(3).应用数轴标根法解不等式要注意等号问题、重根问题。例题解不等式例题解不等式例题例例11：解关于：解关于xx的不等式的不等式1)2(2axaa分析：解答此题的关键是(a2-a-2)的取值（1）当a2-a-2＞0即a<-1或a>2时212aaax(2)当a2-a-2<0时即－1＜a<2时212aaax（3）当a2-a-2＝0时，a=-1或2a=-1时，x∈Ra=2时，x∈Φ返回1.已知一元二次不等式ax2+bx+c>0的解集为{x|20的解集2.解关于x的不等式:x2-(a+a2)x+a3<03.如果只有一个实数满足x2+ax+5≤4，则a=___4.设不等式mx2-2x-m+1<0对于满足|m|≤2一切m值都成立，求x的取值范围5.若xR∈，ax2+bx+a≥-2x2-1恒成立，求a的范围6.已知f(x)=ax2+bx+c(a>0),αβ为方程f(x)=x两根，且0<α<β<1/a；0f(x);(3)αf(x)中，正确的是___________。返回解不等式：1.22123xx127314.222xxxx111.3xx023152.422xxxx11xxax的不等式解关于例1：分析：首先对不等式进行整理，变为：011)1(xxa第一级讨论：0)1(11)x-(ax］［0)1)(11(1xaxa时，)1,11(ax0)1)(11(1xaxa时，1011xxa时，第二级讨论),11()1,(10axa时，),1()11,(0axa时，10xRxa且时，