高考数学专题复习精课件—24同角关系及诱导公式 课件VIP免费

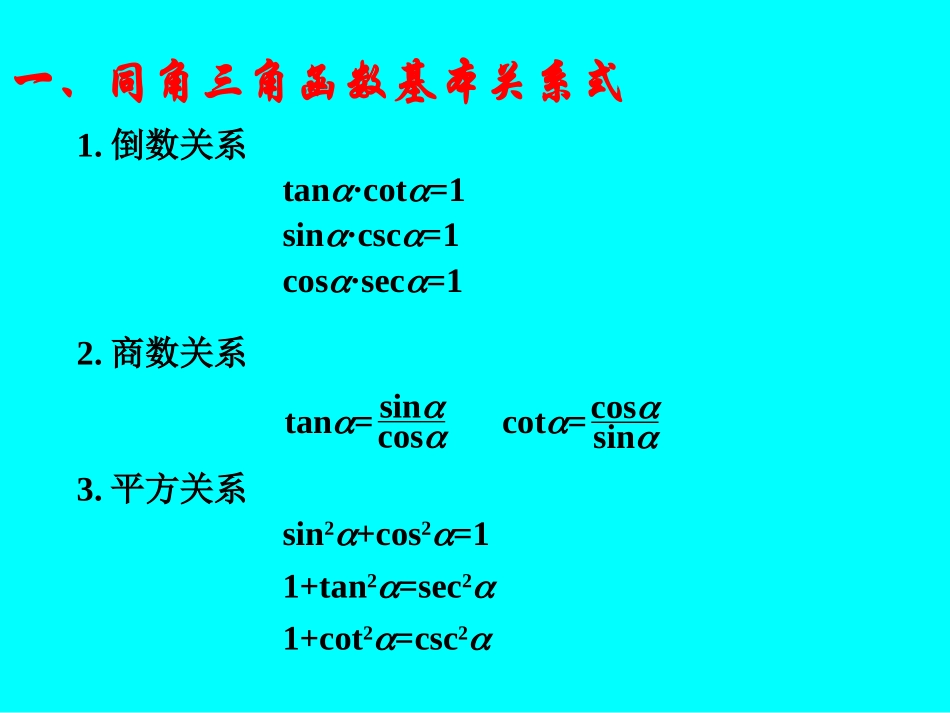
一、同角三角函数基本关系式1.倒数关系2.商数关系3.平方关系tan·cot=1sin·csc=1cos·sec=1sin2+cos2=11+tan2=sec21+cot2=csc2tan=cot=sincoscossin二、诱导公式奇变偶不变,符号看象限.3.本质通过不相等的两个角的同名三角函数或两个互为余函数的三角函数值相等或互为相反数,反映了三角函数的周期性及各种对称性.1.定义2.口诀用自变量的三角函数表示自变量为(kZ)的三角函数的公式叫诱导公式.2k1.已知cot(-)=2,求sin(+)的值.32解: cot(-)=2,又cot(-)=-cot,∴cot=-2.∴是第二或第四象限角,且tan=-.12∴cos2==.1+tan2145又sin(+)=-cos,32255,是第二象限角,255,是第四象限角.-∴sin(+)=32∴cos=255,是第四象限角.255,是第二象限角,-典型例题2.已知cot=m(m0),求cos.解: cot=m(m0),∴角的终边不在坐标轴上.若是第一或第二象限角,则csc=1+cot2=1+m2.∴sin=csc11+m21=.∴cos=sincot=.m1+m21+m2若是第三或第四象限角,则csc=-1+cot2=-1+m2.∴sin=csc11+m21=-.∴cos=sincot=-.m1+m21+m23.已知sin+cos=(0<<),求tan的值.23解法1将已知等式两边平方得sincos=-<0,187 0<<,∴sin>0.∴由sincos<0知cos<0.∴sin-cos=(sin-cos)2=1-2sincos=.43sin+cos=,sin-cos=,4323解方程组得sin=,cos=.2+462-46∴tan==.sincos-9-427解法2将已知等式两边平方得sincos=-<0,187 0<<,∴sin>0.∴由sincos<0知cos<0.∴tan==.sincos-9-427∴sin,cos是方程x2-x-=0的根,且cos为小根.18723∴cos=,sin=.2+462-463.已知sin+cos=(0<<),求tan的值.23解法3由已知sin,,cos成等差数列,设其公差为d,则26∴sin=-d,26cos=+d.26∴由sin2+cos2=1得:(-d)2+(+d)2=1.2626解得d=-或.2323∴tan==.sincos-9-427∴cos=,sin=.2+462-46当d=时,sin=<0,与0<<时sin>0矛盾,232-46∴d=-.233.已知sin+cos=(0<<),求tan的值.234.已知f()=.(1)化简f();sin(-)cos(2-)tan(-+)32cot(--)sin(--)(2)若是第三象限角,且cos(-)=,求f()的值;3215(3)若=-,求f()的值;331解:(1)f()=sincoscot-cotsin=-cos;(2) cos(-)=-sin,32∴由已知可得sin=-.15 是第三象限角,∴cos<0.∴cos=-1-sin2=-256.256∴f()=-cos=.(3) =-=-62+,33153∴f(-)=-cos(-)33133153=-cos(-62+)=-cos53=-cos=-.1235.已知0<<,tan+cot=,求sin(-)的值.522223解: tan+cot=,22sin2∴由已知可得sin=.45 0<<,2cos=1-sin235∴=.∴sin(-)=sincos-cossin333=×-×12354532=(4-33).1016.已知为锐角,且tan=,求的值.sin2cos-sinsin2cos212解: tan=,12又 为锐角,1+tan21∴cos2==.45∴cos=.52∴原式=2sincos2-sin2sincoscos2sincos22sincoscos2=12cos==.547.已知tan(-)=2,求:(1);(2)2sin(3+)cos(+)+sin(-)sin(-).4cos2-3sin2+1sin2-2sincos-cos23252解:(1) tan(-)=2,又tan(-)=-tan,∴tan=-2.∴原式=5cos2-2sin2sin2-2sincos-cos21+tan22tan2-tan=5-2tan2tan2-2tan-1==-.73(2)由(1)知tan=-2,∴原式=2(-sin)(-sin)+(-cos)sin=2sin2-sincos=cos2(2tan2-tan)=2.8.角的终边上的点P与A(a,b)关于x轴对称(a0,b0),角的终边上的点Q与A点关于直线y=x对称,求sinsec+tan∙cot+seccsc的值.解法1依题意P(a,-b),Q(b,a),设r=a2+b2,则:sin=-,sec=,tan=-,cot=,sec=,csc=.brrbbabarara∴原式=-+(-)+brrbbabarara=-1-+=0.a2+b2a2b2a2解法2依题意-=2k+(kZ),即=2k++.22∴原式=sin+tancot(2k++)+cos(2k++)212cos1sin(2k++)21=sin+tan(-tan)+-si...