高考数学复习向导第三章 第2讲 对数式与对数函数课件 理 课件VIP免费

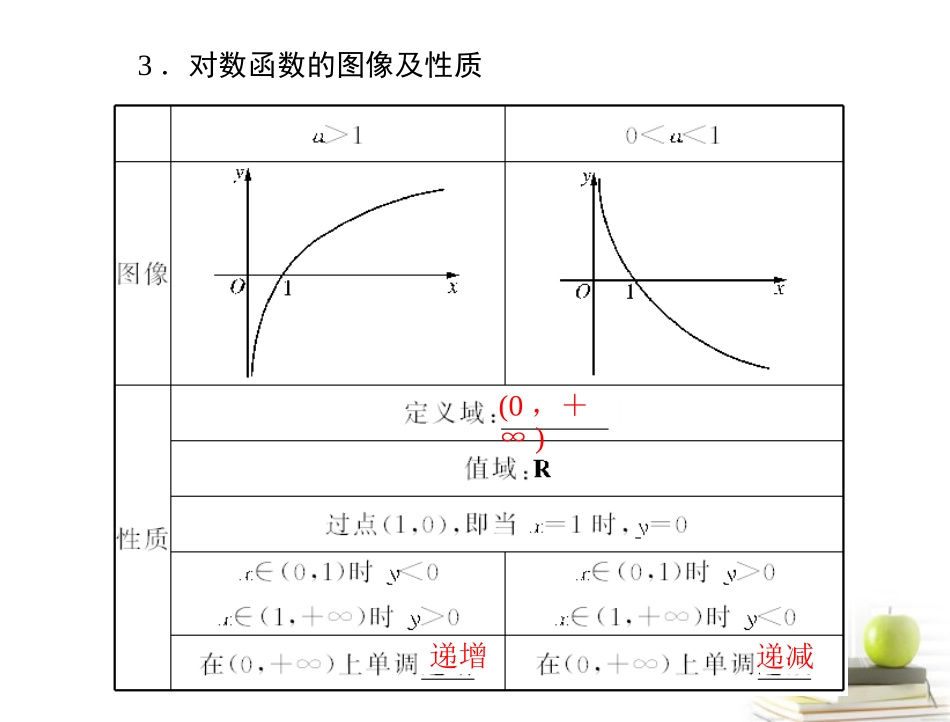
.loga＝第2讲对数式与对数函数1．对数的运算性质loga(MN)＝MN..(M＞0，N＞0，a＞0，a≠1)nlogaMlogaMn＝2．对数换底公式logbN＝(a＞0，a≠1，b＞0，b≠1，N＞0)．logaNlogablogaM＋logaNlogaM－logaN3．对数函数的图像及性质(0，＋∞)递增递减DD1．已知f(3x)＝log29x＋12，则f(1)的值为()A．1B．2C．－1D.122．若log2a＜0，12b＞1，则()A．a＞1，b＞0B．a＞1，b＜0C．0＜a＜1,b＞0D．0＜a＜1,b＜0CDD3．下列指数式与对数式互化不正确的一组是()A．e0＝1与ln1＝0B．138＝12与log812＝－13C．log39＝2与129＝3D．log77＝1与71＝74．已知A＝{x|2≤x≤π}，定义在A上的函数y＝logax(a＞0且a≠1)的最大值比最小值大1，则底数a的值为()A.2πB.π2C．π－2D.π2或2π5．函数y＝log2x－2的定义域是()A．(3，＋∞)B．[3，＋∞)C．(4，＋∞)D．[4，＋∞)lg452lg3＋lg5考点1对数式的运算例1：(1)已知lg2＝a，lg3＝b，用a、b表示log1245＝;(2)(2010年四川)2log510＋log50.25＝()A．0B．1C.2D．4解题思路：设法用对数换底公式将log1245换成常用对数，并且将12与45用2,3来表示．解析：(1)log1245＝＝＝lg122lg2＋lg32b＋1－a2a＋b.点评：对数式的运算一般都是运用对数的运算性质及对数换底公式，在高考中，对数式的运算可能要综合其他知识综合命题．32(2)2log510＋log50.25＝log5100＋log50.25＝log525＝2.故选C.【互动探究】1．(1)已知23a＝49(a>0)，则23loga＝；(2)计算(lg2)2＋lg2·lg50＋lg25＝；(3)若2.5x＝1000,0.25y＝1000，则1x－1y＝.13解析：(1)2332()a＝32223⇒a＝323⇒23loga＝3232log3＝3.(2)原式＝(lg2)2＋(1＋lg5)lg2＋lg52＝(lg2＋lg5＋1)lg2＋2lg5＝(1＋1)lg2＋2lg5＝2(lg2＋lg5)＝2.(3)由2.5x＝1000，得x＝log2.51000.由0.25y＝1000得y＝log0.251000，∴1x－1y＝1log2.51000－1log0.251000＝log10002.5－log10000.25＝log10002.50.25＝log100010＝13.考点2对数函数的图像及性质例2：已知loga2＜logb2,则不可能成立的是()A．a>b>1C．01>a>0D．b>a>1解析：令y1＝logax，y2＝logbx，由于loga2＜logb2，它们的函数图像可能有如图3－2－1三种情况，由图(1)、(2)、(3)，分别得0＜a＜1＜b，a＞b＞1,0＜b＜a＜1.故选D.图3－2－1②③【互动探究】2．对于函数f(x)定义域中任意的x1、x2(x1≠x2)，有如下结论：①f(x1＋x2)＝f(x1)·f(x2)；②f(x1·x2)＝f(x1)＋f(x2)；③fx1－fx2x1－x2>0；④fx1＋x2203－x>0a－x>0x－13－x＝a－x，即a＝－x2＋5x－31134②当35时，f(x)[0,1]∈，log5x>1,y＝f(x)与y＝log5x的图像不再有交点，故选C.图3－2－3错源：复合函数的单调性要考虑函数的定义域例4：已知y＝loga(2－ax)在[0,1]上是关于x的减函数，则a的取值范围是__________．误解分析：忽略单调区间是函数定义域的某个子区间．正解： y＝loga(2－ax)是由y＝logau，u＝2－ax复合而成，又a＞0，∴u＝2－ax在[0,1]上是x的减函数，由复合函数关系知y＝logau应为增函数，∴a＞1.由于x在[0,1]上时y＝loga(2－ax)有意义，u＝2－ax又是减函数，∴只要当x＝1时，u＝2－ax取最小值是umin＝2－a>0即可，∴a＜2.综上可知，所求a的取值范围是1＜a＜2.－1，e－1【互动探究】递增区间为()CA．[0，＋∞)B．(－∞，0]C．[0,2...