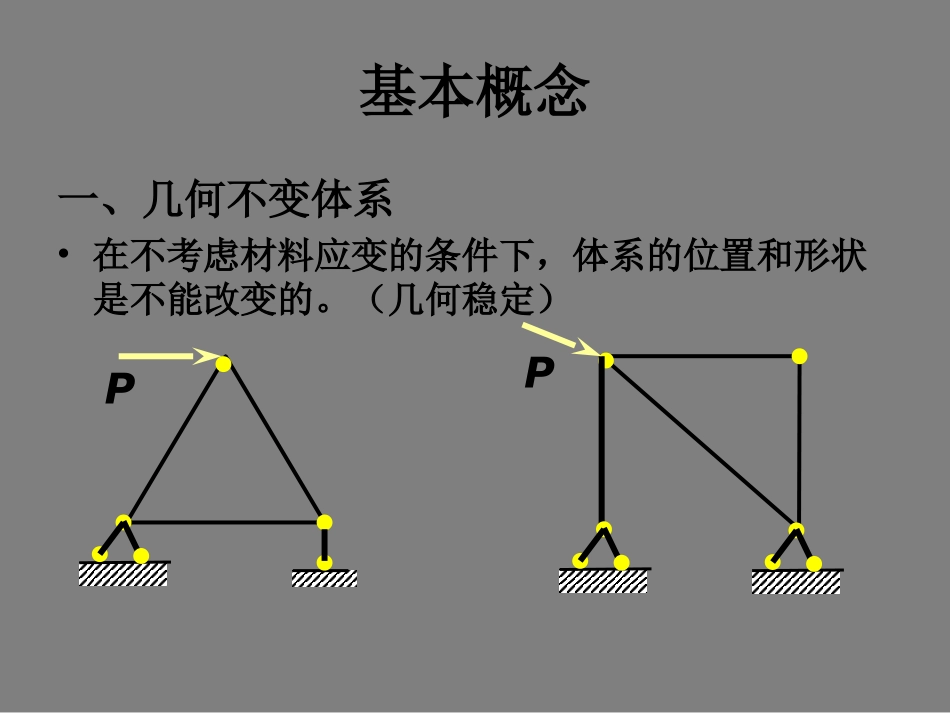
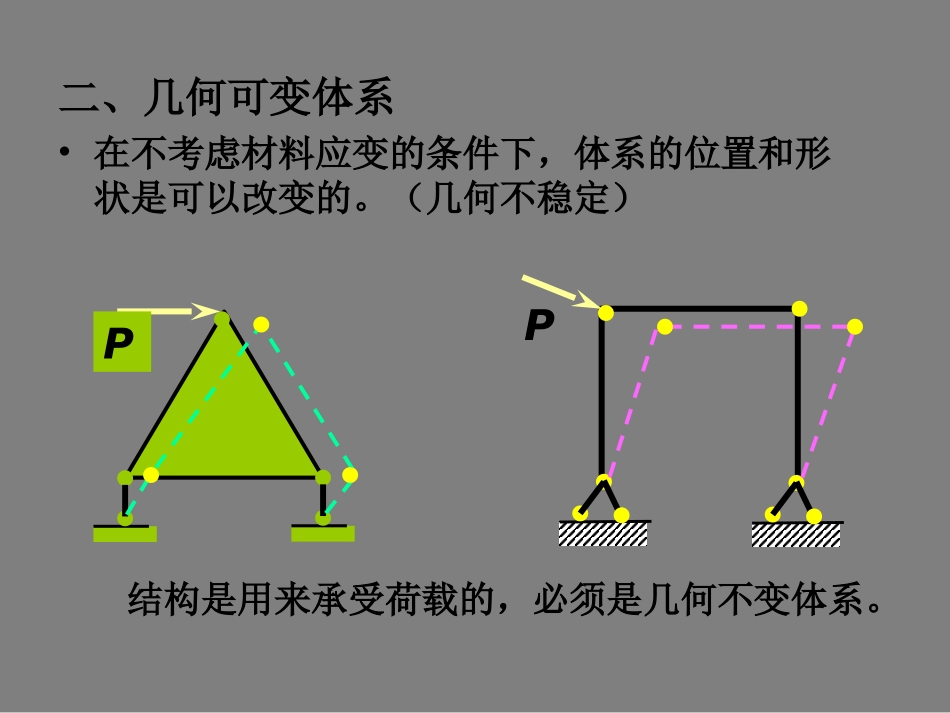
第7章平面体系的几何组成分析基本概念几何组成分析基本概念一、几何不变体系•在不考虑材料应变的条件下,体系的位置和形状是不能改变的。(几何稳定)PP二、几何可变体系•在不考虑材料应变的条件下,体系的位置和形状是可以改变的。(几何不稳定)PP结构是用来承受荷载的,必须是几何不变体系。三、几何组成分析的目的:•决定体系是否可作为结构?•研究结构组成规律,设计新的结构。•确定结构是否静定?从而选择计算方法。五、刚片:•作体系几何组成分析时,不考虑材料应变,将构件视为刚体--刚片。•平面内的一根梁、链杆、任何几何不变的部分。四、几何组成分析的方法:•自由度分析:几何不变的必要条件。•几何组成分析:充分条件。结构几何构造分析——判定体系是否几何可变,对于结构,区分静定和超静定的组成。刚片(rigidplate)——几何形状不变的平面刚体。形状可任意替换平面体系的自由度1.自由度的定义::体系运动时,用来完全确定其位置的独立几何参数(坐标)的数目。2.自由度的确定:3.联系(约束):•能减少自由度的装置•多余约束:加入某种装置,自由度不减少。xyyxA(x,y)o(图1)yx(图2)yoxA(x,y)1、一个点在平面上有两个自由度(图1)。2、一个刚片在平面上有三个自由度(图2)。常见约束:(1)链杆:I•一根链杆减少了一个自由度,为一个联系。xyxy1BACD23(2)单铰:•一个单铰减少了两个自由度,相当于两根链杆,为两个联系。•两根链杆相当于一个单铰。xyxy1BAC2常见约束:(3)复铰:xyxy1BA2D3(4)固定铰:•固定铰为两个联系。xy1BA(5)固定端和刚结点:•为三个联系。有限远虚铰(瞬铰).CODABO’.A实铰A虚铰虚铰无穷远虚铰单铰与链杆的约束关系一个单铰相当于两个链杆。ABCDO虚铰、瞬心ABC实铰ⅠⅡⅠⅡⅠⅡ实铰CDⅠⅡAB无穷远平行⑶必要约束与多余约束必要约束—保持几何不变所必须的约束。多余约束—保持几何不变非必须的约束。绝对必要约束多余约束具有相对性平面体系的几何组成分析一、几何不变体系的组成规则1.规则一(二元体规则)•一个刚片与一个点用两链杆相联,三铰不在一直线上,该体系为几何不变体系,且没有多余约束(一个刚片与一个结点之间的联结)。二元体:两根不在一直线上的链杆与一个结点相联。•在一个刚片上加上或减去一个二元体,并不改变体系的几何不变性或可变性。一、几何不变体系的组成规则2.规则二(两刚片规则)•两刚片用一单铰和一根链杆相联,三铰不在一条直线上,该体系为几何不变体系,且没有多余约束。单铰相当于两个约束•两刚片用三根即不相交于一点又不完全平行的链杆相联,该体系为几何不变体系,且没有多余约束。虚铰两刚片规则两个刚片用不全交于一点也不全平行的三个链杆相联结,或用一个单铰和一个方向不通过单铰的链杆相联结,组成的体系几何不变,且没有多余约束。AⅠⅡBCABC条件不满足时的五种情况瞬变体系平行不等长α1α2α3Δ常变体系平行等长AFCGBEDIIIIIIBA几何不变体系的组成规则3.规则三(三刚片规则)•三刚片用不在同一直线上的单铰相联,该体系为几何不变体系,且没有多余约束。三刚片规则三个刚片用不共线的三个单铰两两相联结,组成的体系几何不变,且没有多余约束。ⅠⅡⅢABCABC瞬变体系ABC常变体系ABCABCCBA条件不满足时的两种情况三刚片规则的变种(a)(b)(c)(e)三个规则可归结为一个三角形法则三刚片规则两刚片规则二元体规则二、瞬变体系•定义:原来为几何可变体系,发生微小位移后成为几何不变体系。瞬间几何可变--瞬变体系二、瞬变体系瞬变体系不可做为结构使用。ABCPFACFABACABPFAC=FAB=P/(2sin)关于几何不变体系的说明:•几何不变体系的组成规则指明了最低限度的联系数目,按照规则组成的体系称为无多余联系的几何不变体系。•体系中联系数目少于规定的数目时,体系成为几何可变体系。•体系中的联系数目多于规定的数目,称为有多余联系的几何不变体系。体系几何可变体系几何不变体系瞬变体系无多余联系的几何不变体系有多余联系的几何不变体系自由度的计算方法1、平面刚片系统:W=3m-3g-2h-b式中:W——自由...