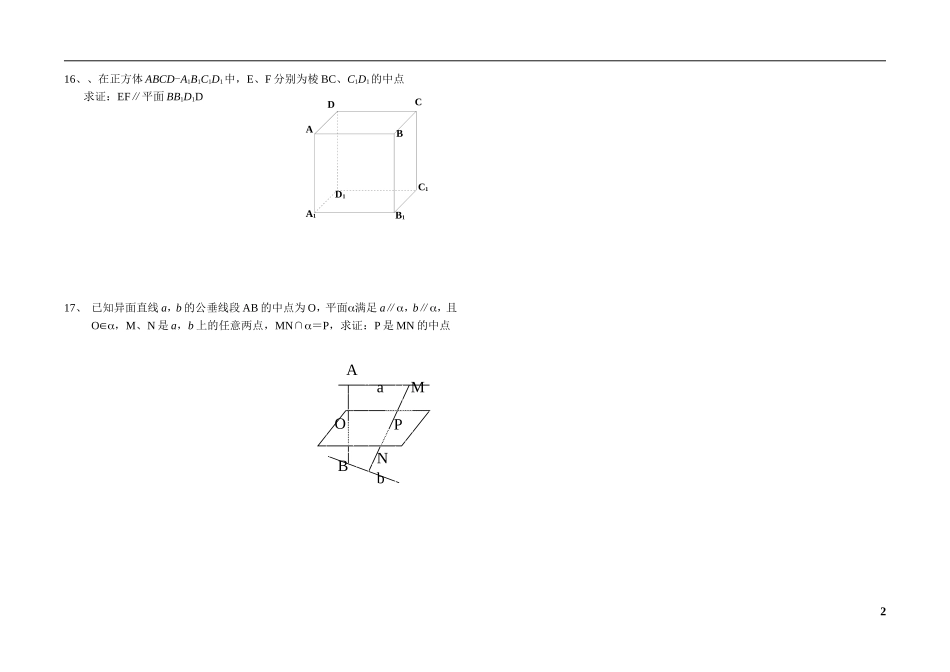
立几面测试 001一、选择题1、以下命题(其中 a,b 表示直线,表示平面)① 若 a∥b,b,则 a∥ ②若 a∥,b∥,则 a∥b③ 若 a∥b,b∥,则 a∥ ④若 a∥,b,则 a∥b 其中正确命题的个数是( )(A)0 个 (B)1 个 (C)2 个 (D)3 个2、已知 m,n 为异面直线,m∥平面,n∥平面,∩=l,则 l( )(A)与 m,n 都相交(B)与 m,n 中至少一条相交(C)与 m,n 都不相交 (D)与 m,n 中一条相交3、已知 a,b 是两条相交直线,a∥,则 b 与的位置关系是 ( ) A、b∥ B、b 与相交 C、bα D、b∥或 b 与相交4、A、B 是直线 l 外的两点,过 A、B 且和 l 平行的平面的个数是( )(A)0 个(B)1 个 (C)无数个 (D)以上都有可能5、直线 a∥平面,点 A∈,则过点 A 且平行于直线 a 的直线( )(A)只有一条,但不一定在平面内 (B)只有一条,且在平面内(C)有无数条,但都不在平面内 (D)有无数条,且都在平面内6、直线 a,b 异面直线, a 和平面平行,则 b 和平面的位置关系是( )(A)b (B)b∥ (C)b 与相交 (D)以上都有可能7、梯形 ABCD 中 AB//CD,AB平面 α,CD平面 α,则直线 CD 与平面 α 内的直线的位置关系只能是 ( )(A)平行 (B)平行和异面 (C)平行和相交 (D)异面和相交8、下列命题中,真命题的个数是 ( ) ① a∥b,a,b 异面,则 b、c 异面 ② a,b 共面,b、c 异面,则 a、c 异面③ a,b 异面,a、c 共面,则 b、c 异面④ a,b 异面,b、c 不相交,则 a、c 不相交 A、0 个 B、1 个 C、2 个 D、4 个二、判断下列命题的真假9、过平面外一点只能作一条直线与这个平面平行( )10、若直线 l,则 l 不可能与平面内无数条直线都相交( ) 11、若直线 l 与平面不平行,则 l 与内任何一条直线都不平行( )12、过两异面直线 a,b 外一点,可作一个平面与 a,b 都平行 ( )三、填空题13、ABCD-A1B1C1D1是正方体,过 A、C、B1三点的平面与底面A1B1C1D1的交线为 l,则 l 与 AC 的位置关系是 。14、已知 P 是正方体 ABCD-A1B1C1D1棱 DD1上任意一点,则在正方体的 12 条棱中,与平面 ABP 平行的是 。三、解答题15、已知 P 是平行四边形 ABCD 所在平面外一点,E、F分...