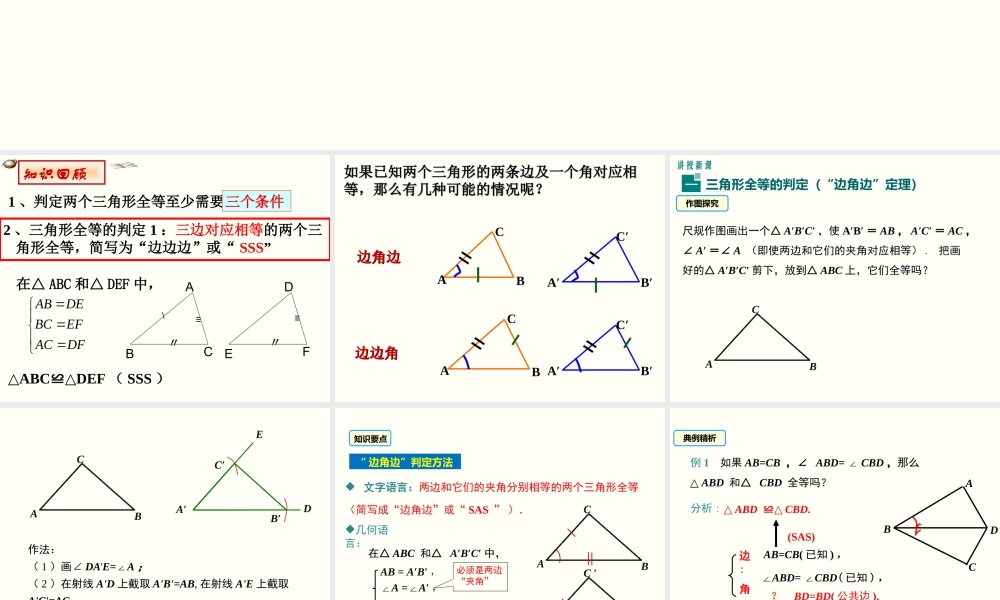
2 、三角形全等的判定 1 :三边对应相等的两个三角形全等,简写为“边边边”或“ SSS”ABCDEF〃〃\≡≡ABDEBCEFACDF在△ ABC 和△ DEF 中,△ABC≌ DEF△( SSS )知识回顾1 、判定两个三角形全等至少需要几个条件?三个条件如果已知两个三角形的两条边及一个角对应相如果已知两个三角形的两条边及一个角对应相等,那么有几种可能的情况呢?等,那么有几种可能的情况呢?CAB 边角边边角边 边边角边边角A′B′C′CAB A′B′C′讲授新课三角形全等的判定(“边角边”定理)一作图探究尺规作图画出一个△ A′B′C′ ,使 A′B′ = AB , A′C′ = AC ,∠ A′ =∠ A (即使两边和它们的夹角对应相等) . 把画好的△ A′B′C′ 剪下,放到△ ABC 上,它们全等吗?A B C A B C A′ D E B′ C′ 作法:( 1 )画∠ DA'E=A∠;( 2 )在射线 A'D 上截取 A'B'=AB, 在射线 A'E 上截取A'C'=AC ;( 3 )连接 B'C '.在△ ABC 和△ A′B′C′ 中,∴ △ ABC ≌ △ A′B′ C′ ( SAS ). 文字语言:两边和它们的夹角分别相等的两个三角形全等(简写成“边角边”或“ SAS ” ).知识要点 “ 边角边”判定方法几何语言:AB = A′B′ ,∠A =∠A′ ,AC =A′C′ ,A B C A ′ B ′ C ′ 必须是两边“夹角”例 1 如果 AB=CB ,∠ ABD= ∠ CBD ,那么 △ ABD 和△ CBD 全等吗?分析 : △ ABD ≌ △ CBD.边:角:边:AB=CB( 已知 ) ,∠ABD= ∠CBD( 已知 ) ,?ABCD(SAS)BD=BD( 公共边 ).典例精析ABCD证明:在△ ABD 和△ CBD 中,AB=CB( 已知 ) ,∠ABD= CBD∠( 已知 ) ,BD=BD( 公共边 ) , △ △ABD ≌ △ CBD ( SAS).想一想: 现在例 1 的已知条件不改变 , 而问题改变成 : 问 AD=CD 吗? BD 平分∠ ABC 吗? 由 △ ABD ≌ △ CBD 可得 AD=CD (全等三角形的对应边相等), BD 平分∠ ADC (全等三角形的对应角相等,∠ ADB=∠CDB ) .例 2 如图,有一池塘,要测池塘两端 A 、 B 的距离,可先在平地上取一个可以直接到达 A 和 B 的点 C ,连接 AC并延长到点 D ,使 CD = CA ,连接 BC 并延长到点 E ,使 CE = CB .连接 DE ,那么量出 DE 的长就是 A 、 B的距离,为什么 ?C·AEDB分析:如果能证明△ ABC≌ △...