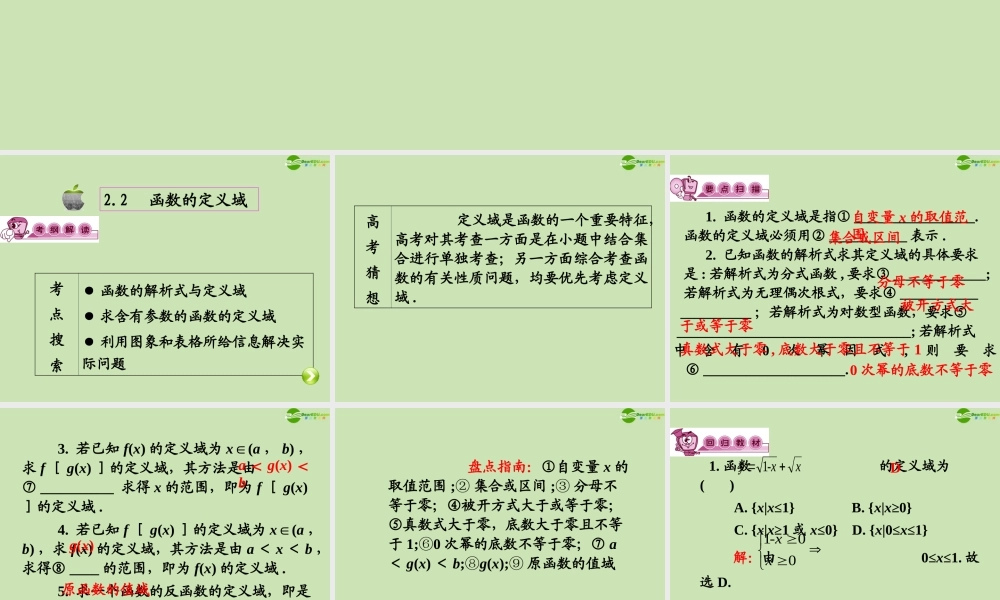
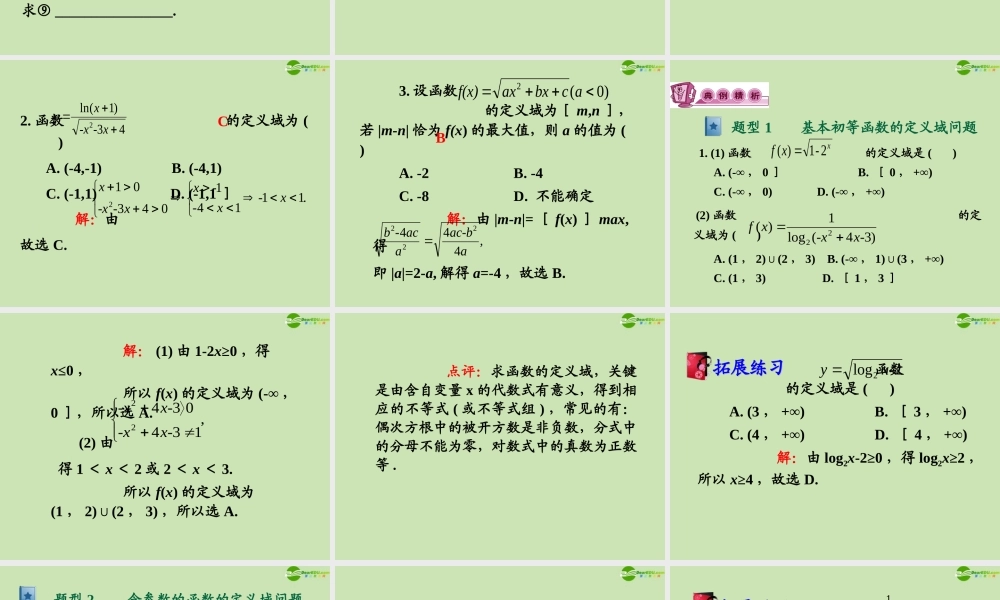
第二章函数考点搜索● 函数的解析式与定义域● 求含有参数的函数的定义域● 利用图象和表格所给信息解决实际问题2.2 函数的定义域高考猜想 定义域是函数的一个重要特征,高考对其考查一方面是在小题中结合集合进行单独考查;另一方面综合考查函数的有关性质问题,均要优先考虑定义域 . 1. 函数的定义域是指① _________________. 函数的定义域必须用② ___________ 表示 . 2. 已知函数的解析式求其定义域的具体要求 是 : 若解析式为分式函数 , 要求③ _____________; 若解析式为无理偶次根式,要求④ ___________ __________ ;若解析式为对数型函数,要求⑤ _________________________________; 若解析式中含有0次幂因式,则要求⑥ ____________________.自变量 x 的取值范围分母不等于零于或等于零集合或区间被开方式大真数式大于零 , 底数大于零且不等于 10 次幂的底数不等于零 3. 若已知 f(x) 的定义域为 x(∈ a , b) ,求 f [ g(x) ]的定义域,其方法是由⑦ __________ 求得 x 的范围,即为 f [ g(x)]的定义域 . 4. 若已知 f [ g(x) ]的定义域为 x(∈ a ,b) ,求 f(x) 的定义域,其方法是由 a < x < b ,求得⑧ ____ 的范围,即为 f(x) 的定义域 . 5. 求一个函数的反函数的定义域,即是求⑨ ________________.a < g(x) <bg(x)原函数的值域 盘点指南:①自变量 x 的取值范围 ;② 集合或区间 ;③ 分母不等于零;④被开方式大于或等于零;⑤真数式大于零,底数大于零且不等于 1;0⑥ 次幂的底数不等于零;⑦ a< g(x) < b;⑧g(x);⑨ 原函数的值域 1. 函数 的定义域为( ) A. {x|x≤1} B. {x|x≥0} C. {x|x≥1 或 x≤0} D. {x|0≤x≤1} 解:由 0≤x≤1. 故选 D.Dx-xy 1001x-x2. 函数 的定义域为 ( ) A. (-4,-1) B. (-4,1) C. (-1,1) D. (-1,1 ] 解:由故选 C.C43)1(ln2x--xxy.x-x--xx--xx11141043012 3. 设函数 的定义域为[ m,n ],若 |m-n| 恰为 f(x) 的最大值,则 a 的值为 ( ) A. -2 B. -4 C. -8 D. 不能确定 解:由 |m-n|= [ f(x) ] max, 得 即 |a|=2-a, 解得 a=-4 ,故选 B.B0)(2acbxaxf(x),aac-baac-b444222 1. (1) 函数 的定义域是 ( ) A. (-∞ , 0 ] B. [...