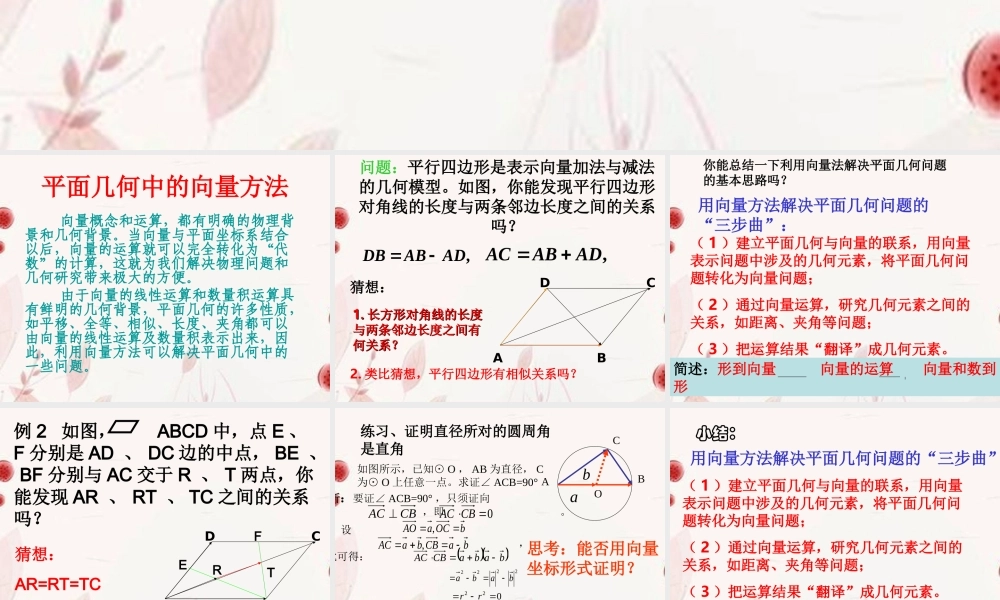
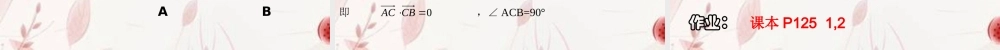2.5 平面向量应用举例2.5.1 平面几何的向量方法平面几何中的向量方法 向量概念和运算,都有明确的物理背景和几何背景。当向量与平面坐标系结合以后,向量的运算就可以完全转化为“代数”的计算,这就为我们解决物理问题和几何研究带来极大的方便。 由于向量的线性运算和数量积运算具有鲜明的几何背景,平面几何的许多性质,如平移、全等、相似、长度、夹角都可以由向量的线性运算及数量积表示出来,因此,利用向量方法可以解决平面几何中的一些问题。问题:平行四边形是表示向量加法与减法的几何模型。如图,你能发现平行四边形对角线的长度与两条邻边长度之间的关系吗?,ACABAD�,DBABAD�ABCD猜想:1.1. 长方形对角线的长度长方形对角线的长度与两条邻边长度之间有与两条邻边长度之间有何关系?何关系?2. 类比猜想,平行四边形有相似关系吗?你能总结一下利用向量法解决平面几何问题的基本思路吗?( 1 )建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;( 2 )通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;( 3 )把运算结果“翻译”成几何元素。用向量方法解决平面几何问题的“三步曲”:简述:形到向量 向量的运算 向量和数到形例 2 如图, ABCD 中,点 E 、F 分别是 AD 、 DC 边的中点, BE 、 BF 分别与 AC 交于 R 、 T 两点,你能发现 AR 、 RT 、 TC 之间的关系吗?ABCDEFRT猜想:AR=RT=TC练习、证明直径所对的圆周角是直角ABCO如图所示,已知⊙ O , AB 为直径, C为⊙ O 上任意一点。求证∠ ACB=90°分析:要证∠ ACB=90° ,只须证向量 ,即 。CBAC 0CBAC解:设 则 ,由此可得:bOCaAO ,baCBbaAC,babaCBAC2222baba022rr即 ,∠ ACB=90°0CBAC思考:能否用向量坐标形式证明?a b( 1 )建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;( 2 )通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;( 3 )把运算结果“翻译”成几何元素。小结:用向量方法解决平面几何问题的“三步曲”:作业:课本 P125 1,2