高中数学：对数函数(1)课件(苏教版必修1) 课件VIP免费

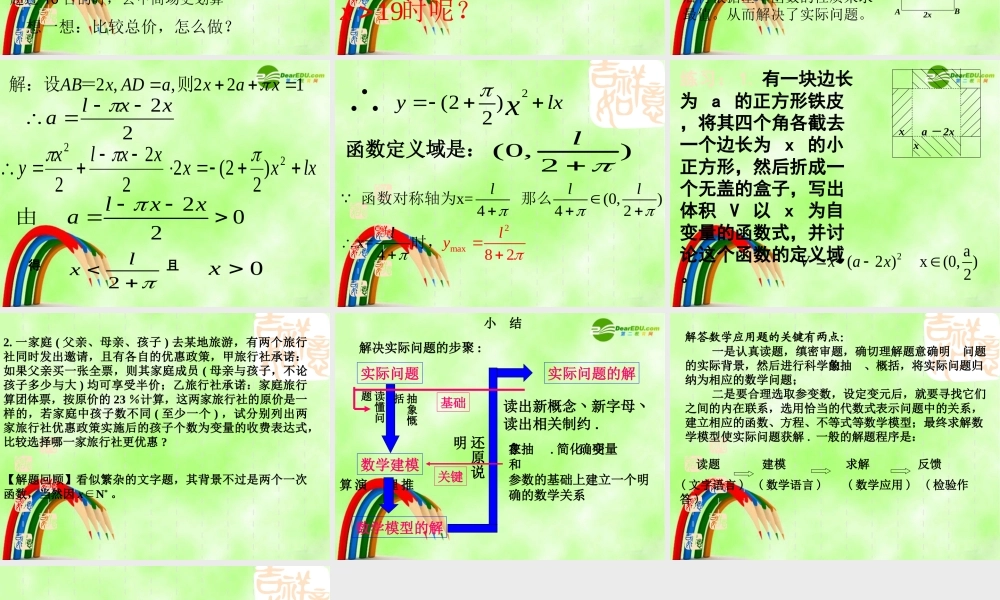
引言： 素质教育呼唤应用意识，近几年来的高考试题增强了对密切联系生产和生活实际的应用性问题的考查力度，突出对能力的考查——重视应用，培养应用数学的意识，培养分析问题的解决问题的能力。 分析近几年高考应用性问题不难得出，试题从实际出发提供公平背景，设问新颖、灵活，而解决这些问题所涉及的数学知识、数学思想和方法又都是高中数学大纲所要求掌握的概念、公式、定理和法则等基础知识和基本方法。 例 1. 有一批影碟机 (VCD) 原销售价为每台 800 元 , 在甲丶乙两家商场均有销售 , 甲商场用如下的方法促销 : 买一台单价为 780 元 , 买两台每台都为 760 元 , 依 此类推 , 每多买一台则所买各台单价均再减少 20 元 , 但每台最低价不能低于 440 元 ; 乙商场一律都按原价的 75% 销售 某单位需购买一批此类影碟机 , 问去哪家商场购买花费较少 ?分析思路 : （ 1 ）可以比较 x 台每台的单价。 （ 2 ）也可以比较 x 台的总价。 118x 题目中每台单价的限制知：(1) 若在甲商场买 x 台每台须多少元 ?(800 - 20x ) 元80020440x我想买 20 台，多少钱一台800 20 118 x440 x 19 x xxNN xN  (2). 去乙商场买 x 台 , 每台要多少钱 ?800 75%600  +当1 x 18时：800－20x-6000 1 x 10 xN所以买少于 10 台的时，到乙商场去买更便宜买 10 台时，甲，乙商场一样超过 10 台的时，去甲商场更划算想一想：比较总价，怎么做？ 当 y>0 时，即 时 , 去乙商场购买比去甲商场购买要便宜110x Y = (800 - 20x)x - 600x = 118x  - 20x2 + 200xx=10 时 y=0 ：甲，乙商场价格一样1910xx 时，甲商场更便宜时呢？例 2 ：用长为 L 的铝合金弯成下部为矩形，上部为半圆形的框架，若矩形底边长为 2x ，求此框架的面积 y 与 x 的函数式，并写出它的定义域和面积的最大值。 ABCD2xO2x分析：利用初中学过的平面几何知识建立函数关系式，然后再根据基本函数的性质来求最值。从而解决了实际问题。22xxlalxxxxxlxy22)22(22222 ,,221ABx ADaxax解：设＝则2 02lxxa由 2lx0x得且 2(2)2ylxx函数定义域是： (0,)2l2max x= (0,)442x82= 4llllyl 函数对称轴为...