高三数学第一轮总复习 5.3 向量的坐标运算课件(2) 课件VIP免费

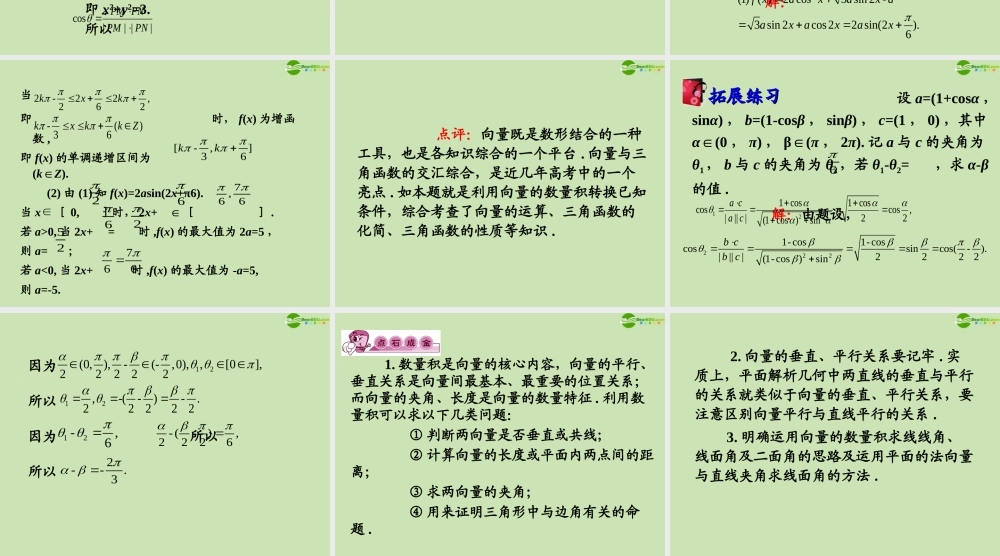
第五章平面向量5.3 向量的坐标运算 第二课时题型 4 向量的夹角 1. 在平面直角坐标系内，已知向量 =(2 ， 1) ， =(1 ， 7) ， =(5 ， 1).若 Z 为直线 OP 上一个动点，当 取最小值时，求 cos∠AZB 的值 .OP�OA�OB�ZA ZB� 解：因为 Z 在直线 OP 上，所以 与 共线，所以又因为 =(1-2λ ， 7-λ) ，同理 =(5-2λ ， 1-λ) ，所以， =(1-2λ)(5-2λ)+(7-λ)(1-λ) =5(λ-2)2-8 ，所以当 λ=2 时， ( )min=-8.此时 =(-3 ， 5) ， =(1 ， -1) ，OZ�OP�(2 , )().OZOPR  �-ZAOA OZ�ZB�ZA ZB�ZA ZB�ZA�ZB�2222-84 17cos-.(-3)5 1(-1)17AZB  点评：利用坐标向量求向量夹角的有关问题时，运用坐标运算先求其数量积与模的积，其中涉及到参数时，一般是转化为函数问题后，利用函数的性质进行求解，这正体现了知识之间的纵横联系 . 已知 M(-1 ， 0) ，N(1 ， 0) ，动点 P 使得 求 与 的夹角 θ 的取值范围 . 解：因为 由已知 | |=2 ，所以 =2. 设点 P(x ， y) ，则 =(-1-x ， -y) ， =(1-x ， -y) ，所以 (-1-x)(1-x)+y2=2 ， 即 x2+y2=3. 所以拓展练习拓展练习22,MNPM PN�PM�PN�22,MNPM PN�MN�PM PN�PM�PN�cos|| ||PM PNPMPN��因为 0≤x2≤3 ，所以 4-x2∈ ［ 1 ， 2 ］，从而 cosθ∈ ［ ， 1 ］ , 所以 θ∈ ［ 0, ］ .222222(1)(1- )21.424-24-xyxyxxx123 2. 已知 x∈R, 向量 f(x)= ， a≠0. (1) 求函数 f(x) 的解析式，并求当 a>0 时，f(x) 的单调递增区间； (2) 当 x∈ ［ 0, ］时， f(x) 的最大值为5 ，求 a 的值 . 解： 题型 5 三角函数坐标运算与三角函数交汇22( cos,1),(2, 3 sin- ),OAaxOBax a�OA OB�22(1) ( )2 cos3 sin 2 -3 sin 2cos22 sin(2).6f xaxax aaxaxax当即 时， f(x) 为增函数 ,即 f(x) 的单调递增区间为 (k∈Z). (2) 由 (1) 知 f(x)=2asin(2x+π6).当 x∈ ［ 0, ］时， 2x+ ∈ ［ ］ .若 a>0, 当 2x+ = 时 ,f(x) 的最大值为 2a=5 ，则 a= ；若 a<0, 当 2x+ 时 ,f(x) 的最大值为 -a=5,则 a=-5.2-22,262kxk-()36kxkkZ [-,]36kk ...