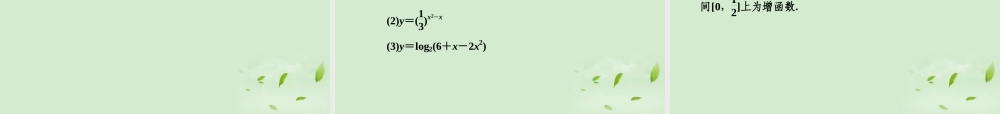第 三 节函数的单调性与最值 重点难点 重点:①函数单调性的定义. ②函数的最大(小)值. 难点:①函数单调性的证明. ②求复合函数单调区间. 知识归纳 一、单调性定义 1.单调性定义:设函数 f(x)的定义域为 I,区间 D⊆ I,若对于任意的 x1,x2∈D,当 x1f(x2),则 f(x)为区间 D 上的减函数. 2.证明函数的单调性一般从定义入手,也可以用导数证明. (1)利用定义证明函数单调性的一般步骤是: ①任取 x1、x2∈D,且 x10,则 f(x)在区间 D 内为增函数;如果 f ′(x)<0,则 f(x)在区间 D 内为减函数. 二、单调性的有关结论 1.若 f(x),g(x)均为增(减)函数,则 f(x)+g(x)仍为增(减)函数. 2.若 f(x)为增(减)函数,则-f(x)为减(增)函数,如果同时有 f(x)>0,则 1fx为减(增)函数, fx为增(减)函数. 3.互为反函数的两个函数有相同的单调性. 4.y=f[g(x)]是定义在 M 上的函数,若 f(x)与 g(x)的单调性相同,则其复合函数 f[g(x)]为增函数;若 f(x)、g(x)的单调性相反,则其复合函数 f[g(x)]为减函数. 5.奇函数在关于原点对称的两个区间上的单调性相同;偶函数在关于原点对称的两个区间上的单调性相反. 三、函数单调性的应用有: (1)比较函数值或自变量值的大小. (2)求某些函数的值域或最值. (3)解证不等式. (4)作函数图象. 四、函数的最大(小)值: 1.定义:一般地,设函数 y=f(x)定义域为Ⅰ,如果存在实数 M 满足: (1)对任意 x∈Ⅰ,都有 f(x)≤M(或 f(x)≥M); (2)存在 x0∈Ⅰ,使得 f(x0)=M. 称 M 是函数 y=f(x)的最大(或最小)值. 2.求法: (1)配方法,(2)判别式法,(3)基本不等式法,(4)换元法,(5)数形结合法,(6)单调性法,(7)导数法. 误区警示 1.对于函数单调性定义的理解,要注意以下三点 (1)函数的单调性是对某一个区间而言的.f(x)在区间A 与 B 上都是增(或减)函数,在 A∪B 上不一定单调. (2)单调性是函数在某一区间上的性质,因此定义中的 x1,x2在这一区间上具有任意性,不能用特殊值代替. 2.在研究函数的单调性时,应先确...