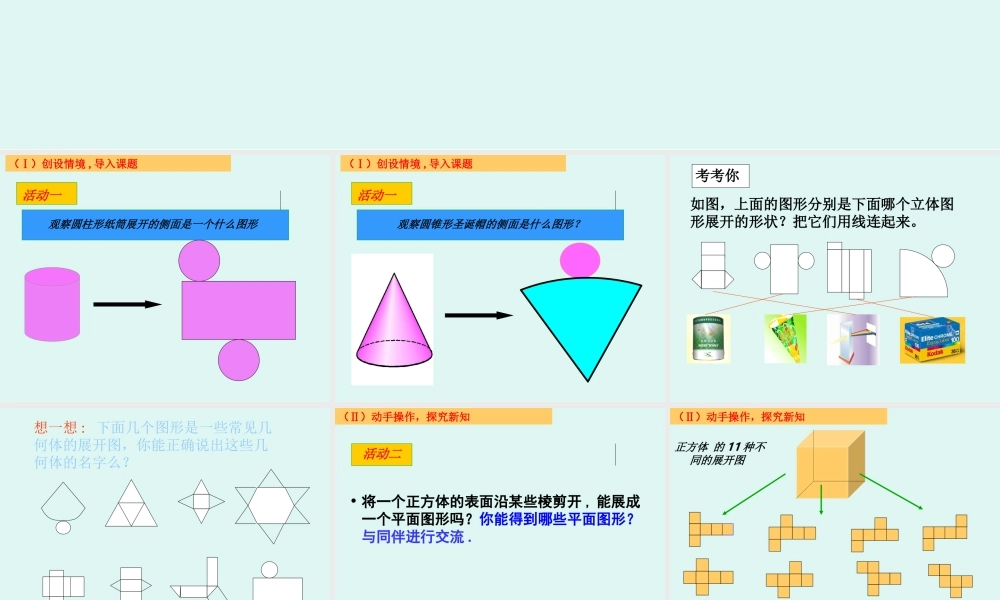
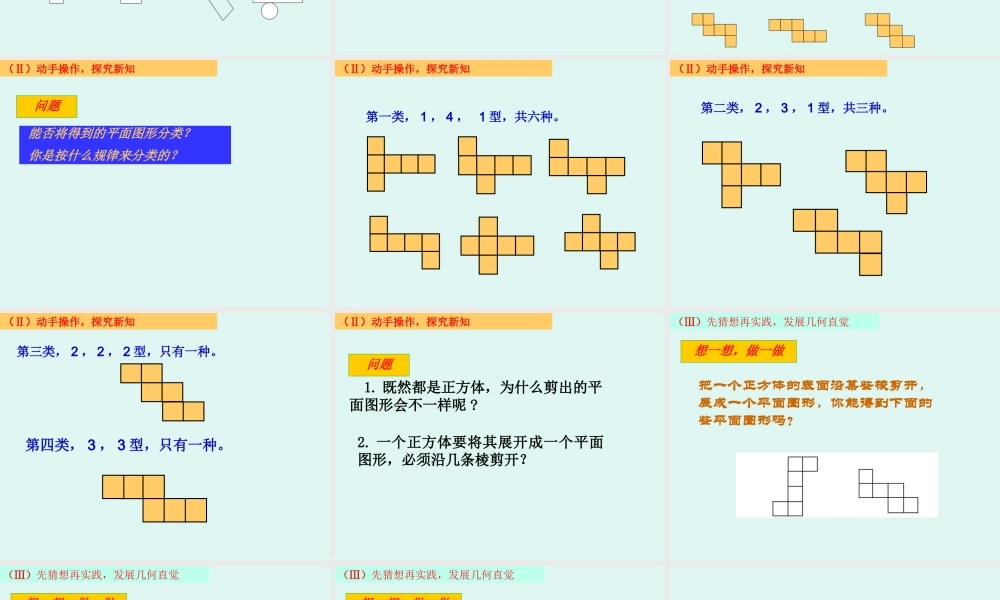
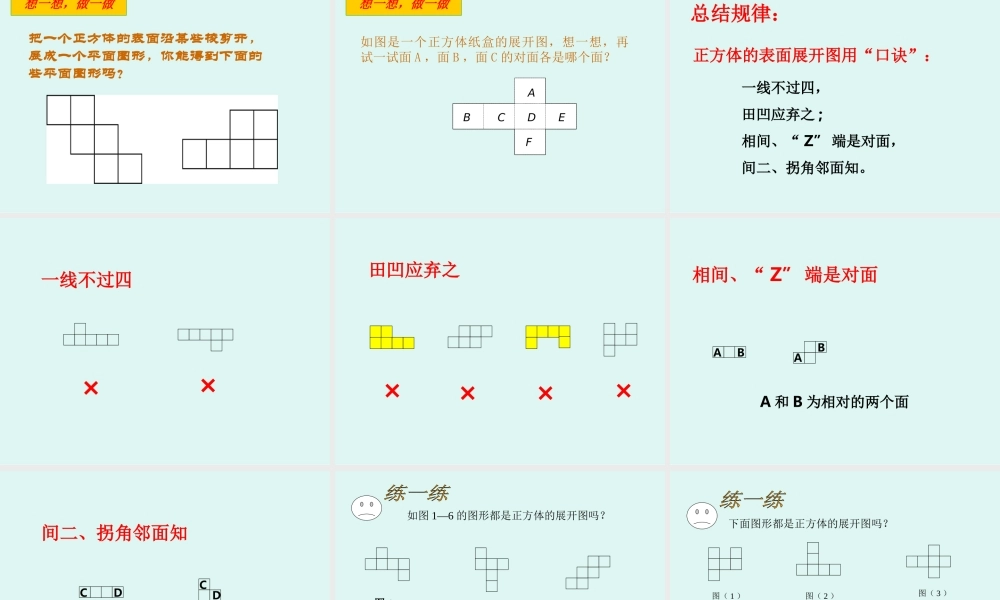
展开与折叠 (2) (Ⅰ)创设情境 , 导入课题 活动一观察圆柱形纸筒展开的侧面是一个什么图形 (Ⅰ)创设情境 , 导入课题 活动一观察圆锥形圣诞帽的侧面是什么图形? 如图,上面的图形分别是下面哪个立体图形展开的形状?把它们用线连起来。考考你 想一想 : 下面几个图形是一些常见几何体的展开图,你能正确说出这些几何体的名字么? 活动二• 将一个正方体的表面沿某些棱剪开 , 能展成一个平面图形吗?你能得到哪些平面图形?与同伴进行交流 .(Ⅱ)动手操作,探究新知 (Ⅱ)动手操作,探究新知正方体 的 11 种不同的展开图 (Ⅱ)动手操作,探究新知能否将得到的平面图形分类?你是按什么规律来分类的? 问题 第一类, 1 , 4 , 1 型,共六种。(Ⅱ)动手操作,探究新知 第二类, 2 , 3 , 1 型,共三种。(Ⅱ)动手操作,探究新知 第三类, 2 , 2 , 2 型,只有一种。第四类, 3 , 3 型,只有一种。(Ⅱ)动手操作,探究新知 2. 一个正方体要将其展开成一个平面图形,必须沿几条棱剪开? 1. 既然都是正方体,为什么剪出的平面图形会不一样呢 ?(Ⅱ)动手操作,探究新知问题 (Ⅲ)先猜想再实践,发展几何直觉 把一个正方体的表面沿某些棱剪开,展成一个平面图形,你能得到下面的些平面图形吗?想一想,做一做 (Ⅲ)先猜想再实践,发展几何直觉 把一个正方体的表面沿某些棱剪开,展成一个平面图形,你能得到下面的些平面图形吗?想一想,做一做 (Ⅲ)先猜想再实践,发展几何直觉 想一想,做一做如图是一个正方体纸盒的展开图,想一想,再试一试面 A ,面 B ,面 C 的对面各是哪个面? ABCDEF 正方体的表面展开图用“口诀”:一线不过四,田凹应弃之 ;相间、“ Z” 端是对面,间二、拐角邻面知。总结规律: 一线不过四×× 田凹应弃之×××× 相间、“ Z” 端是对面ABABA 和 B 为相对的两个面 间二、拐角邻面知CCDDC 和 D 为相邻的两个面 如图 1—6 的图形都是正方体的展开图吗?图 1图 2图 3图 4图 5图 6是是是是不是不是 下面图形都是正方体的展开图吗?图( 1 )图( 2 )图( 3 )图( 4 )图( 5 )图( 6 )不是不是是不是不是不是 如图是一个正方体纸盒的展开图,请在图中的 6 个正方形中分别填入 1 、 2 、3 、 -1 、 -2 、 -3 ,时展开图沿虚线折叠成正方体后相对面上的两个数互为相反数。 下面是一个...