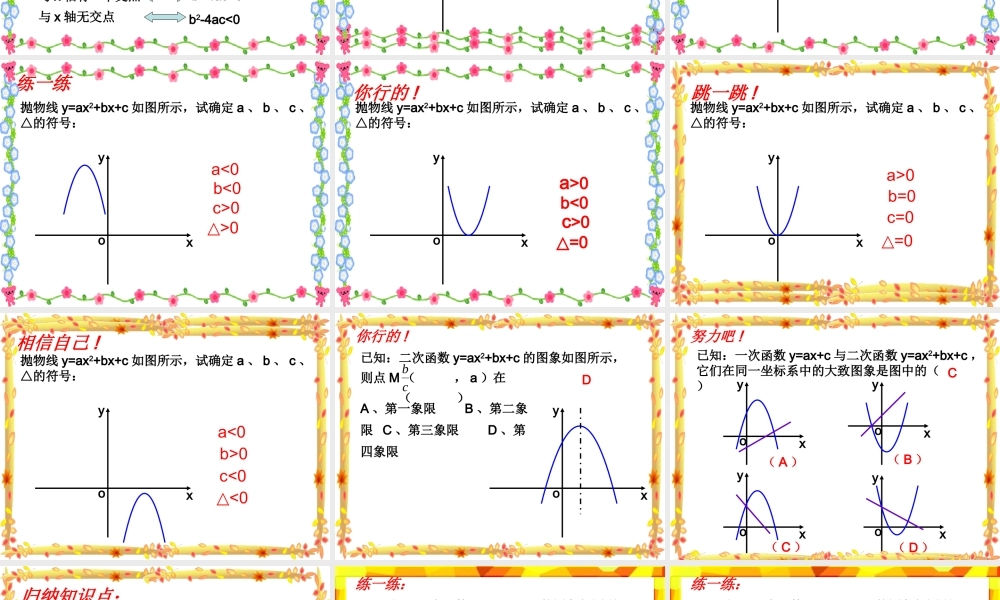
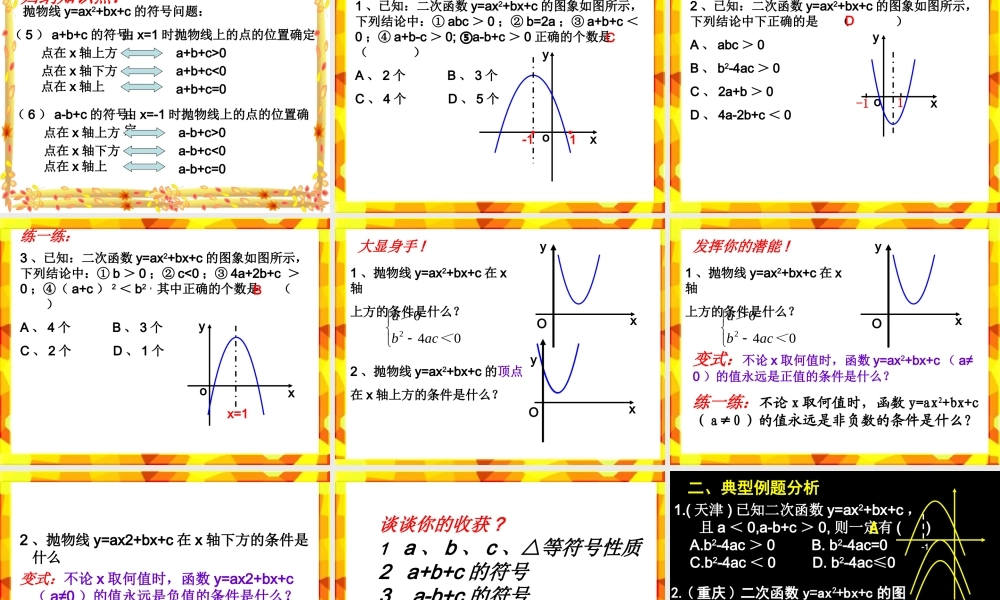
二次函数的符号问题二次函数的符号问题( a 、 b 、 c 、△等符号)学习目标1. 会根据二次函数的图像判断一些代数式的符号 . 2. 灵活的掌握二次函数的图像与系数之间的关系3. 培养学生的审美观点及二次函数的对称美 .回味知识点:1 、抛物线 y=ax2+bx+c 的开口方向与什么有关?2 、抛物线 y=ax2+bx+c 与 y 轴的交点是 .3 、抛物线 y=ax2+bx+c 的对称轴是 .复习知识点:抛物线 y=ax2+bx+c 的符号问题:( 1 ) a 的符号:由抛物线的开口方向确定开口向上a>0开口向下a<0( 2 ) C 的符号:由抛物线与 y 轴的交点位置确定交点在 x 轴上方c>0交点在 x 轴下方c<0经过坐标原点c=0( 3 ) b 的符号:由对称轴的位置确定对称轴在 y 轴左侧a 、 b 同号对称轴在 y 轴右侧a 、 b 异号对称轴是 y 轴b=0( 4 ) b2-4ac 的符号:由抛物线与 x 轴的交点个数确定与 x 轴有两个交点b2-4ac>0与 x 轴有一个交点b2-4ac=0与 x 轴无交点b2-4ac<0试一试抛物线 y=ax2+bx+c 如图所示,试确定 a 、 b 、 c 、△的符号:xyoa>0 b<0 c>0 △>0做一做抛物线 y=ax2+bx+c 如图所示,试确定 a 、 b 、 c 、△的符号:xyoa>0 b>0 c=0 △>0 练一练抛物线 y=ax2+bx+c 如图所示,试确定 a 、 b 、 c 、△的符号:xyoa<0 b<0 c>0 △>0 你行的 !抛物线 y=ax2+bx+c 如图所示,试确定 a 、 b 、 c 、△的符号:xyoa>0 b<0 c>0 △=0跳一跳 !抛物线 y=ax2+bx+c 如图所示,试确定 a 、 b 、 c 、△的符号:xyoa>0 b=0 c=0 △=0相信自己 !抛物线 y=ax2+bx+c 如图所示,试确定 a 、 b 、 c 、△的符号:xyoa<0 b>0 c<0 △<0 你行的 !已知:二次函数 y=ax2+bx+c 的图象如图所示,则点 M ( , a )在 ( )A 、第一象限 B 、第二象限 C 、第三象限 D 、第四象限 cbxoyD已知:一次函数 y=ax+c 与二次函数 y=ax2+bx+c ,它们在同一坐标系中的大致图象是图中的( )努力吧 !xyoxyoxyoxyo( A )( B )( C )( D )C归纳知识点:抛物线 y=ax2+bx+c 的符号问题:( 5 ) a+b+c 的符号:由 x=1 时抛物线上的点的位置确定点在 x 轴上方点在 x 轴下方点在 x 轴上a+b+c>0a+b+c<0a+b+c=0( 6 ) a-b+c 的符号:由 x=-1 时抛物线上的点的位置确定点在 x 轴上方点在 x 轴下方点在 x 轴上a-b+c>0...