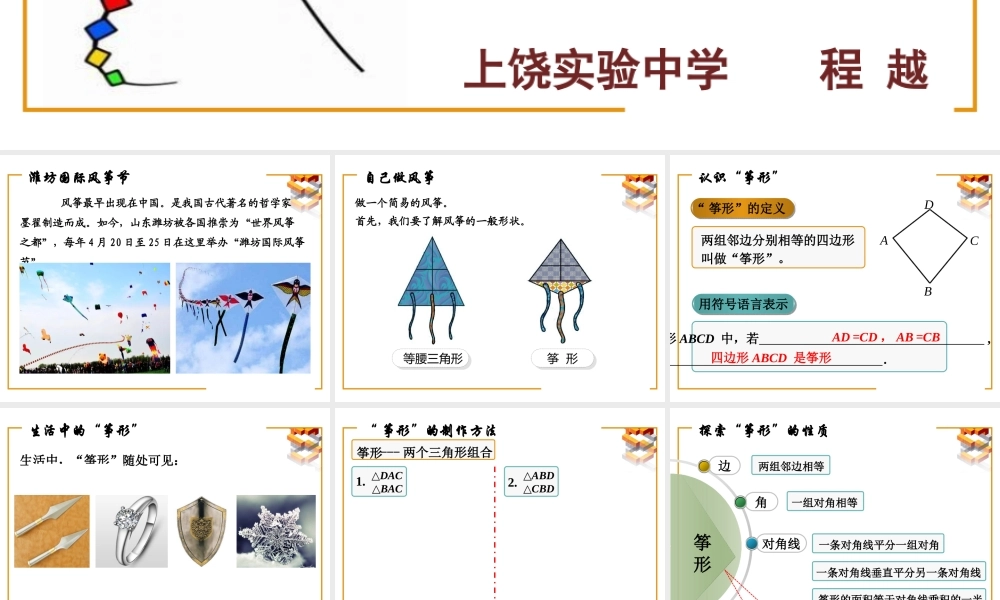
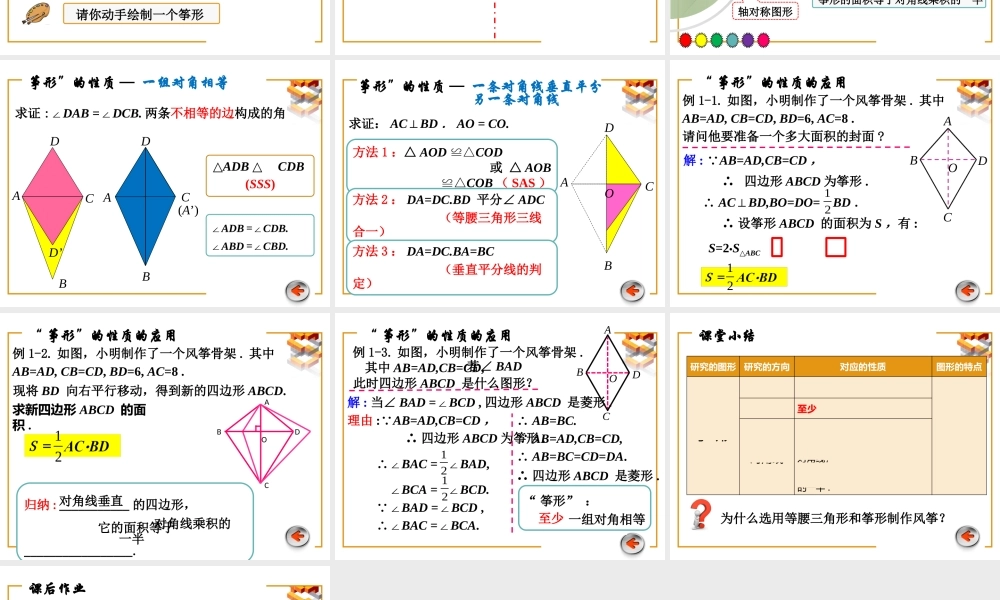
上饶实验中学 程 越用全等三角形研究“筝形”第十二章 数学活动 2 风筝最早出现在中国。是我国古代著名的哲学家墨翟制造而成。如今,山东潍坊被各国推崇为“世界风筝之都”,每年 4 月 20 日至 25 日在这里举办“潍坊国际风筝节”潍坊国际风筝节自己做风筝等腰三角形等腰三角形筝 形筝 形做一个简易的风筝。首先,我们要了解风筝的一般形状。DABC认识“筝形”“ 筝形”的定义两组邻边分别相等的四边形叫做“筝形”。用符号语言表示在四边形 ABCD 中,若 ,则 .四边形 ABCD 是筝形 AD =CD , AB =CB生活中的“筝形”生活中,“筝形”随处可见:请你动手绘制一个筝形DACBDACB“ 筝形”的制作方法△DAC△BAC1.△ABD△CBD2.筝形--- 两个三角形组合探索“筝形”的性质边角对角线筝形两组邻边相等一组对角相等一条对角线平分一组对角一条对角线垂直平分另一条对角线筝形的面积等于对角线乘积的一半轴对称图形DACBD’求证 :DAB ∠=DCB.∠DACB(A’)两条不相等的边构成的角筝形”的性质 — 一组对角相等△ADB △CDB (SSS)∠ADB =CDB. ∠∠ABD =CBD.∠DACO 求证: AC⊥BD . AO = CO.B方法 1 :△ AOD ≌△COD 或 △ AOB ≌△COB ( SAS )筝形”的性质 — 一条对角线垂直平分 另一条对角线方法 2 : DA=DC.BD 平分∠ ADC (等腰三角形三线合一) 方法 3 : DA=DC.BA=BC (垂直平分线的判定) 例 1-1. 如图,小明制作了一个风筝骨架 . 其中AB=AD, CB=CD, BD=6, AC=8 .请问他要准备一个多大面积的封面 ?解 : AB=AD,CB=CD , ∴ 四边形 ABCD 为筝形 . ∴ AC⊥BD,BO=DO= BD . ∴ 设筝形 ABCD 的面积为 S ,有 :AB CDO 12S=2•S△ABC = 2× AC•BO= AC•BD= 24 .121212“ 筝形”的性质的应用例 1-2. 如图,小明制作了一个风筝骨架 . 其中AB=AD, CB=CD, BD=6, AC=8 .请问他要准备一个多大面积的封面 ?OCDB求新四边形 ABCD 的面积 .12A现将 BD 向右平行移动,得到新的四边形 ABCD.归纳 : ___________ 的四边形, 它的面积等于_________________.“ 筝形”的性质的应用对角线垂直 对角线乘积的一半解 : 当∠ BAD =∠BCD , 四边形 ABCD 是菱形 .理由 : AB=AD,CB=CD , ∴ 四边形 ABCD 为筝形 . ∴∠BAC = ∠BAD, ∠BCA = ∠BCD. ∠BAD =∠BCD , ∴∠BAC =∠BCA.1212 ∴ AB=BC. AB=AD,CB=CD,...