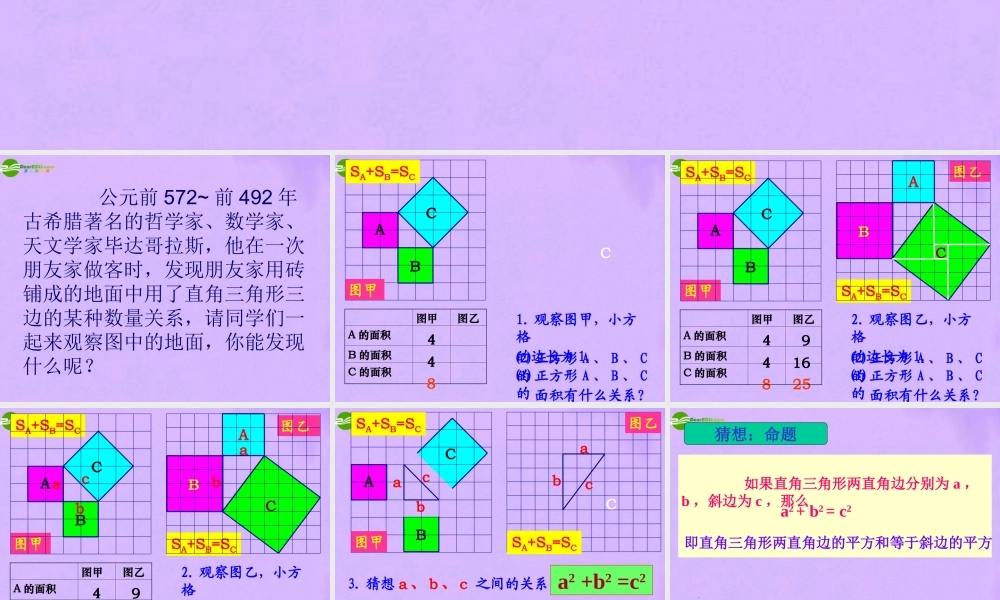
公元前 572~ 前 492 年古希腊著名的哲学家、数学家、天文学家毕达哥拉斯,他在一次朋友家做客时,发现朋友家用砖铺成的地面中用了直角三角形三边的某种数量关系,请同学们一起来观察图中的地面,你能发现什么呢?BAC图甲图乙A 的面积B 的面积C 的面积448SA+SB=SCC图甲1. 观察图甲,小方格的边长为 1.⑴ 正方形 A 、 B 、 C的 面积各为多少?⑵ 正方形 A 、 B 、 C的 面积有什么关系?ABC图乙2. 观察图乙,小方格的边长为 1.⑴ 正方形 A 、 B 、 C的 面积各为多少?91625SA+SB=SC⑵ 正方形 A 、 B 、 C的 面积有什么关系?448ABCSA+SB=SC图甲图甲图乙A 的面积B 的面积C 的面积CAB图乙2. 观察图乙,小方格的边长为 1.91625SA+SB=SC⑵ 正方形 A 、 B 、 C的 面积有什么关系?448ABCSA+SB=SC图甲图甲图乙A 的面积B 的面积C 的面积abcabcCABCC图乙SA+SB=SCSA+SB=SC图甲abcabc3. 猜想 a 、 b 、 c 之间的关系?a2 +b2 =c2猜想:命题 如果直角三角形两直角边分别为 a ,b ,斜边为 c ,那么a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方.做一做 分别以 3 厘米、4 厘米为直角三角形的直角边做出一个直角三角形,并测量斜边的长度 .前面得到的规律对这个三角形还成立吗?∟abc用这四个三角形拼一拼、摆一摆,看看是否能得到一个含有以斜边 c 为边长的正方形,并与同伴交流。∟abc∟abc∟abcbababa bacccc大正方形的面积该怎样表示 ?(a+b)2 =a2 + b2 + 2ab = c2+2ab可得 : a2 + b2 = c21. 利用面积 (1)2142cab 勾股定理 如果直角三角形两直角边分别为 a ,b ,斜边为 c ,那么a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方 .勾股定理揭示了直角三角形三边之间的关系 . 读一读 我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦 . 所以,这个定理叫做勾股定理。下图称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的 . 此图是北京召开的 2002 年国际数学家大会( TCM - 2002 )的会标,其图案正是“弦图”,它反映了中国古代的数学成就 . 图 1-1图 1-2 1. 如图,你能解决这个问题吗?35x┓ 如果知道了直角形任意两边的长度,能不能利用勾股定理求第三边的长度呢?学以致用学以致用2x1结论变形直角三角形中,两直角边的平方和等于斜边的平方...