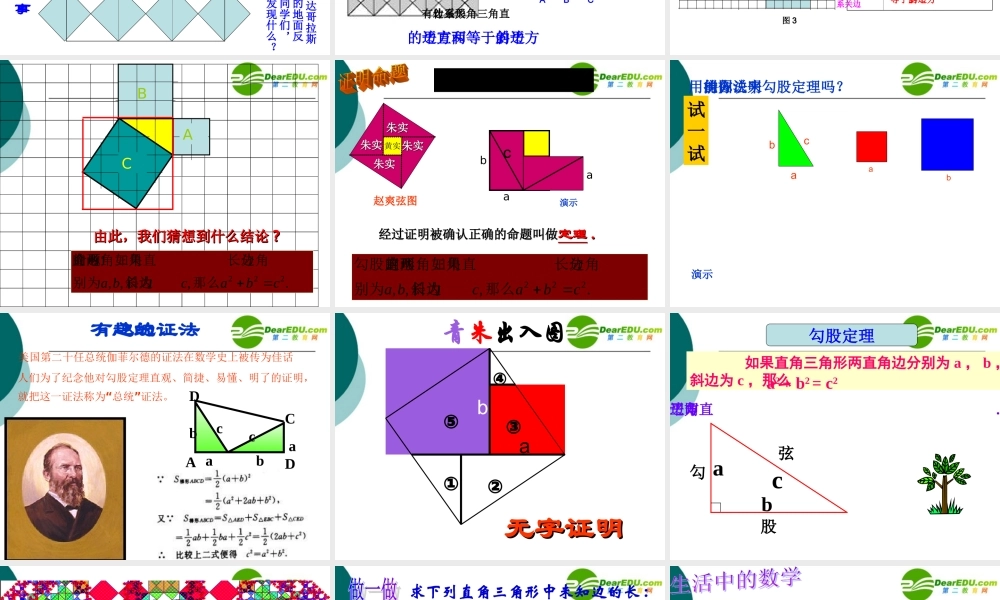
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。 —— 毕达哥拉斯 东营区史口镇中心中学 古宝针1. 体验勾股定理的探索过程,学习古今中外数学家的探索精神。2. 会运用勾股定理解决简单的实际问题。数学家毕达哥拉斯的故事 相传两千五百年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么? 数学家毕达哥拉斯的发现:A 、 B 、 C 的面积有什么关系?直角三角形三边有什么关系?SA+SB=SC两直边的平方和等于斜边的平方ABCABCA 的面积 ( 单位面积)B 的面积 ( 单位面积)C 的面积 ( 单位面积)图 2图 3A 、 B、 C 面积关系直角三角形三边关系图 2图 3491392534sA+sB=sC两直角边的平方和等于斜边的平方探究与猜想 是不是所有的直角三角是不是所有的直角三角形的三边都满足这种关系形的三边都满足这种关系呢呢 ??ABCABC由此,我们猜想到什么结论由此,我们猜想到什么结论 ??.,,, 1222cbacba那么斜边长为别为角边长分如果直角三角形的两直命题黄实朱实朱实朱实朱实朱实朱实朱实朱实ba22:ba 它们的面积和a.,,, 1222cbacba那么斜边长为别为角边长分如果直角三角形的两直命题.,,, :222cbacba那么斜边长为别为角边长分如果直角三角形的两直勾股定理经过证明被确认正确的命题叫做经过证明被确认正确的命题叫做定理定理 ..演示C赵爽弦图试一试你能用拼图的方法来说明勾股定理吗?abcab演示 美国第二十任总统伽菲尔德的证法在数学史上被传为佳话人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,“”就把这一证法称为 总统 证法。 有趣的总统证法bcabcaADCD abc无字证明无字证明①②③④⑤青朱出入图 如果直角三角形两直角边分别为 a , b ,斜边为 c ,那么a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方.勾股定理cab勾股弦11比一比看看谁算得快!求下列直角三角形中未知边的长 :可用勾股定理建立方程 .方法小结 :8x171620x125x1. 如图 , 一个高 3 米 , 宽 4 米的大门 , 需在相对角的顶点间加一个加固木条 , 则木条的长为 ( )A.3 米 B.4 米 C.5 米 D.6 米C342 、如图 : 是一个长方形零件图, 根据所给的尺寸 , 求两孔中心A 、 B 之间的距离ABC409016040 3. 小明的妈妈买了一部29 英寸( 74 厘米)的电视机。小明量...