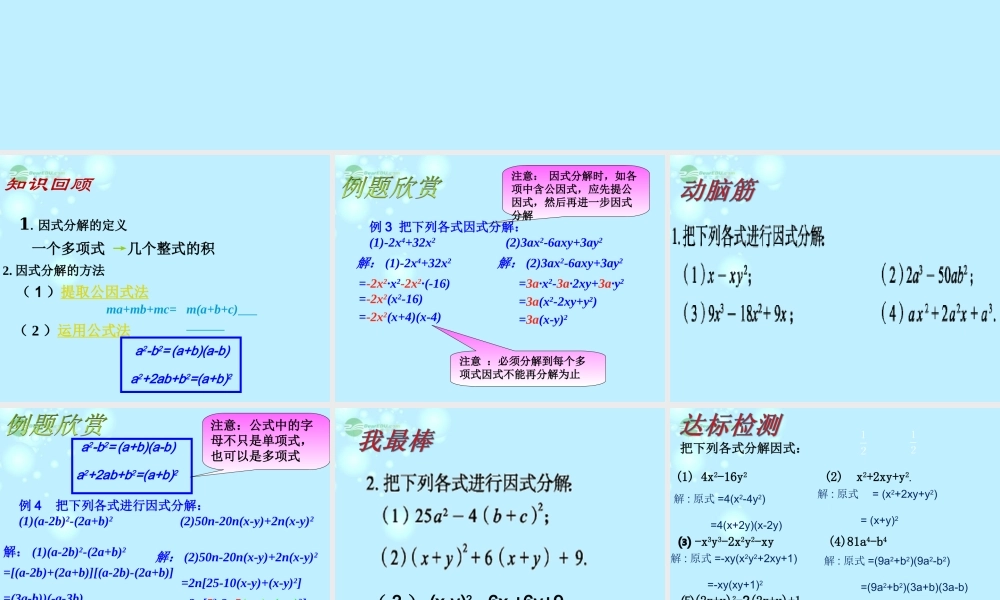
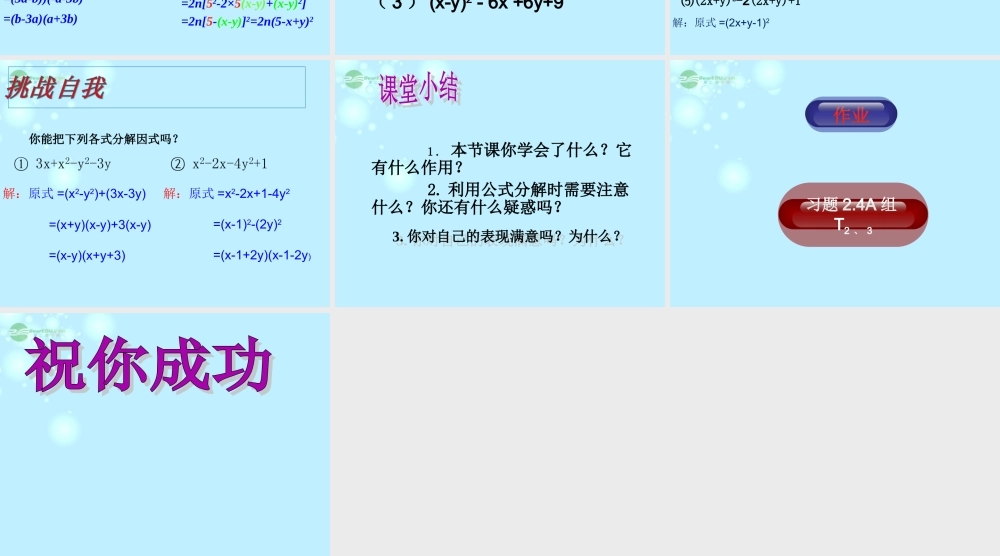
知识回顾1.因式分解的定义 一个多项式 →几个整式的积2. 因式分解的方法( 1 )提取公因式法( 2 )运用公式法ma+mb+mc= m(a+b+c) a2-b2= (a+b)(a-b)a2+2ab+b2=(a+b)2 例 3 把下列各式因式分解:(1)-2x4+32x2 (2)3ax2-6axy+3ay2解: (1)-2x4+32x2=-2x2·x2-2x2·(-16)=-2x2(x2-16)=-2x2(x+4)(x-4)=3a·x2-3a·2xy+3a·y2=3a(x2-2xy+y2)=3a(x-y)2解: (2)3ax2-6axy+3ay2注意: 因式分解时,如各项中含公因式,应先提公因式,然后再进一步因式分解注意 :必须分解到每个多项式因式不能再分解为止 a2-b2= (a+b)(a-b)a2+2ab+b2=(a+b)2 例 4 把下列各式进行因式分解:(1)(a-2b)2-(2a+b)2 (2)50n-20n(x-y)+2n(x-y)2解: (1)(a-2b)2-(2a+b)2=[(a-2b)+(2a+b)][(a-2b)-(2a+b)]=(3a-b))(-a-3b)=(b-3a)(a+3b)解: (2)50n-20n(x-y)+2n(x-y)2=2n[25-10(x-y)+(x-y)2]=2n[52-2×5(x-y)+(x-y)2]=2n[5-(x-y)]2=2n(5-x+y)2注意:公式中的字母不只是单项式,也可以是多项式( 3 ) (x-y)2 - 6x +6y+9把下列各式分解因式: ⑶ -x3y3-2x2y2-xy(1) 4x2-16y2 (2) x2+2xy+y2.(4)81a4-b4 1212⑸(2x+y)2-2(2x+y)+1解 : 原式 =4(x2-4y2) =4(x+2y)(x-2y)1212解 : 原式 = (x2+2xy+y2) = (x+y)2解 : 原式 =-xy(x2y2+2xy+1) =-xy(xy+1)2解 : 原式 =(9a2+b2)(9a2-b2) =(9a2+b2)(3a+b)(3a-b)解:原式 =(2x+y-1)2 你能把下列各式分解因式吗?解:原式 =(x2-y2)+(3x-3y)=(x+y)(x-y)+3(x-y)=(x-y)(x+y+3)解:原式 =x2-2x+1-4y2 =(x-1)2-(2y)2 =(x-1+2y)(x-1-2y) 1 . 本节课你学会了什么?它有什么作用? 2. 利用公式分解时需要注意什么?你还有什么疑惑吗?3. 你对自己的表现满意吗?为什么?3. 你对自己的表现满意吗?为什么?作业习题 2.4A 组T2 、 3