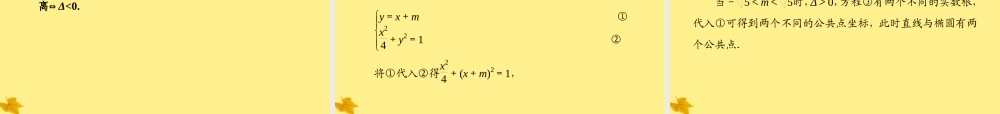•第 2 课时 椭圆方程及性质的应用•1. 通过椭圆标准方程的求法,体会一元二次方程的根与系数的关系的应用.•2. 掌握椭圆的离心率的求法及其范围的确定.•3. 掌握点与椭圆、直线与椭圆的位置关系,并能利用椭圆的有关性质解决实际问题 .•1. 椭圆的方程和性质的应用及直线和椭圆的位置关系,相关的距离、弦长、中点等问题是考查的重点.•2. 本节内容常与方程、不等式、平面向量、解三角形等结合命题,命题的形式多样化 .•直线与圆的位置关系有相切、相离、相交.判断直线与圆的位置关系有两种方法:•(1) 几何法:利用圆心到直线的距离 d 与半径 r 的关系判断,当 d = r 时,直线与圆相切;当 d>r 时,直线与圆相离;当d0 时,直线与圆相交.当 Δ<0 时,直线与圆相离.•你知道直线与椭圆的位置关系吗?点与椭圆、直线与椭圆的位置关系 (1)点 P(x0,y0)与椭圆x2a2+y2b2=1(a>b>0)的位置关系: 点 P 在椭圆上⇔ x20a2+y20b2=1; 点 P 在椭圆内部⇔ x20a2+y20b2<1; 点 P 在椭圆外部⇔ x20a2+y20b2>1. (2)直线 y=kx+m 与椭圆x2a2+y2b2=1(a>b>0)的位置关系判断方法:联立 y=kx+mx2a2+y2b2=1,∴消 y 得一个一元二次方程 位置关系解的个数Δ 的取值相交 解Δ 0相切 解Δ 0相离 解Δ 0两一无>=<1.已知点(2,3)在椭圆x2m2+y2n2=1 上,则下列说法正确的是( ) A.点(-2,3)在椭圆外 B.点(3,2)在椭圆上 C.点(-2,-3)在椭圆内 D.点(2,-3)在椭圆上 •答案: D解析: 4m2+ 9n2=1,则点(-2,3)、点(-2,-3)、点(2,-3)在椭圆上.故选 D. 2.直线 y=x+2 与椭圆x2m+y23=1 有两个公共点,则 m的取值范围是( ) A.m>1 B.m>1 且 m≠3 C.m>3 D.m>0 且 m≠3 解析: 由 y=x+2x2m+y23=1得(3+m)x2+4mx+m=0 Δ=(4m)2-4(3+m)×m>0, 解得 m>1 或 m<0(舍去). 答案: B 3.已知点(4,2)是直线 l 被椭圆x236+y29=1 所截得的线段的中点,则 l 的方程是________. 解析: 设截得的线段为 AB,A(x1,y1),B(x2,y2),中点坐标为(x0,y0),利用“点差法”得y21-y22x21-x22=- 936, 即y1-y2x1-x2·y0x0=- 936,∴k=y1-y2x1-x2=-12, ∴直线 l...