九年级数学(新高一)暑假辅导数学讲义 三角形内角和外角平分线定理课件 人教新课标版 课件VIP免费

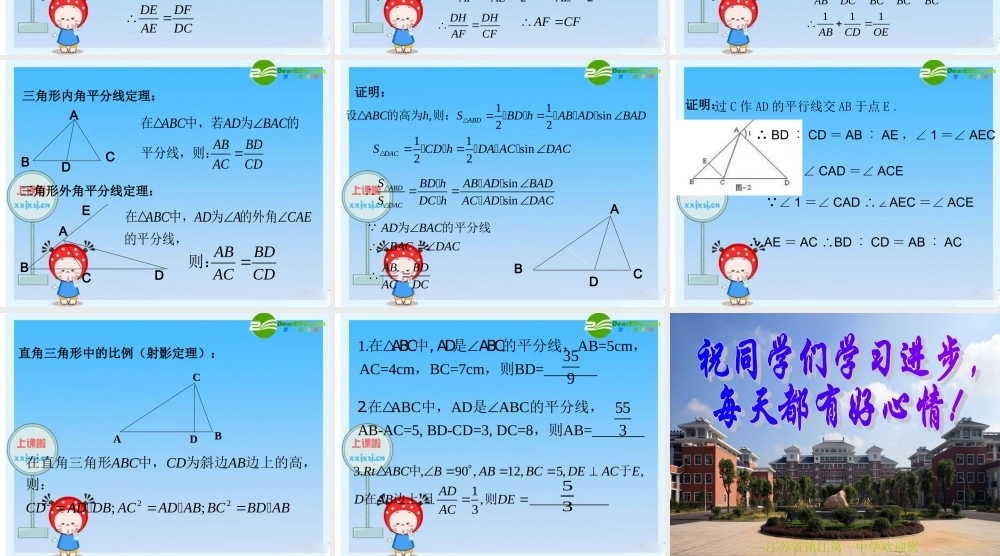
本节内容是关于几何中的一些比例关系，这几节内容现在在初中课本中已“淡化”，但是这几个结论在高中的“立体几何”和“平面解析几何”中有时会用到 . 因此 , 在本节中首先把这几个定理内容介绍给同学们 , 然后利用这三个定理来解决一些题目 . 其中对于“平行线分线段成比例”介绍几条稍有难度的题目，而“三角形内外角平分线性质定理”和“直角三角形中的比例”的题目直接围绕定理展开，难度不大 . 平行线分线段成比例定理三条平行线截两条直线，截得的对应线段成比例 定理的基本图形：如图，因为 AD BE CF∥∥， 所以 AB ： BC=DE ： EF; AB ： AC=DE ： DF ； BC ： AC=EF ： DF 也可以说 AB ： DE=BC ： EF ； AB ： DE=AC ： DF ； BC ： EF=AC ： DF 推 论 的 基 本 图形 :ABCDEFABCDEABCDEABCDEABAD平行线分线段成比例定理推论 : 平行于三角形一边的直线截其他两边 ( 或两边的延长线），所得的对应线段成比例 例 1 ：DCDFAEDE DCDFAEDE DCDFAEDE DCDFAEDE DCDFAEDE DCDFAEDE ABCDEF证明：FDEDFAEDC如图， 是平行四边形ABCD边CD上一点，连结BF，并延长BF交AD的延长线于点E. 求证：ABCD 四边形为平行四边形CD ABAD BC，DEEFAEEB（平行于三角形一边的直线截其他两边， 所得的对应线段成比例）同理可得 :EFDFEBDCDEDFAEDC 例 2 ：1,ABCAD,B ,2BACF.: AF=CFDEEEAEE如图 在中， 为中线上的一点，连结延长交于点 求证ABCDEFH证明： DHAC,BFH作交于点DHBDCFBC（平行于三角形的一边，并且和其他两边相交的直线所截得的三角形的三边与原三角形三边对应成比例。） DBC是的中点12DHBDCFBC12DEAE 12DHDEAFAE同理可得：DHDHAFCFAFCF 例3111ABDCOE如图，已知：AB CD, AC, BD交于O, OE AB交BC于E. 求证：证明：OEAB(1)OECEABBCOEDC(2)OEBEDCBC121OEOECEBEBCABDCBCBCBC（）（ ）得：111ABCDOE 三角形内角平分线定理：ABCDABCADBACABBDACCD在中，若为的平分线，则：三角形外角平分线定理：ABCDEABCADACAE在中，为的外角的平分线，ABBDACCD则： 证明：11,sin22ABDABChSBD hAB ADBAD设的高为则：11sin22DACSCD hDA ACDACsinsinABDDACSBD hAB ADBADSDC hAC ADDAC...