八年级数学 勾股定理 课件VIP免费

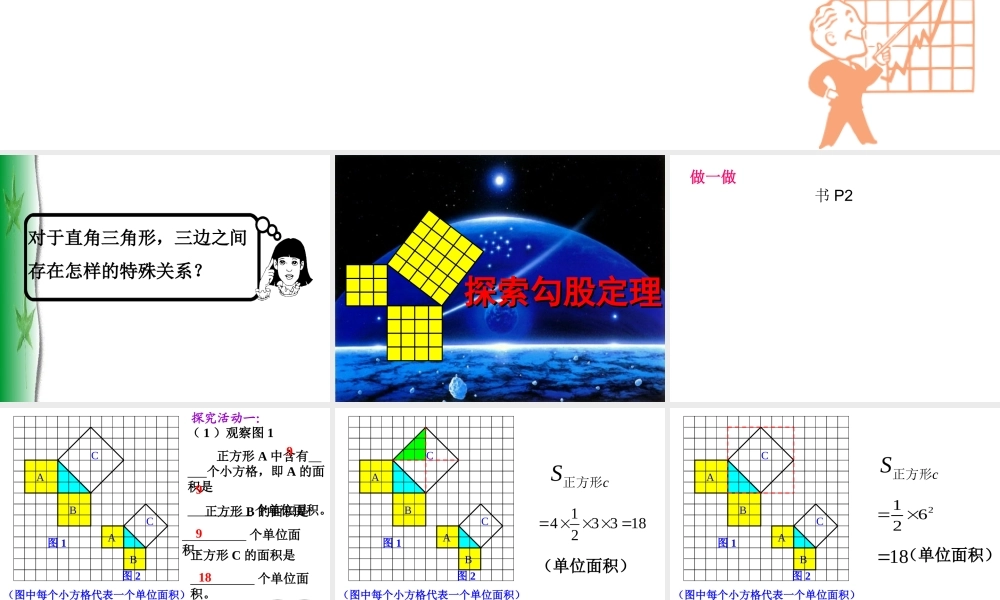
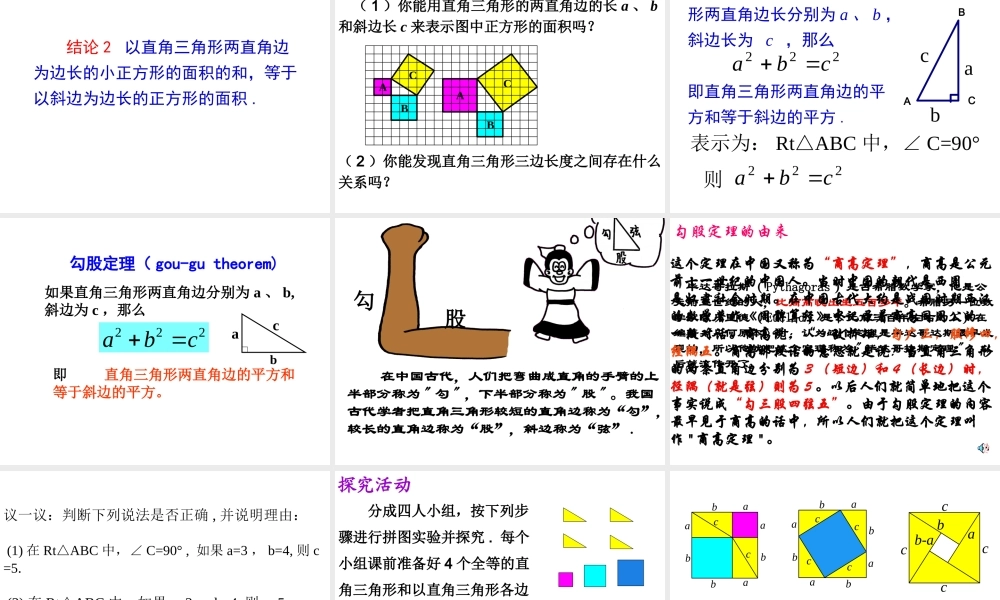
复习提问 任意三角形三边满足怎样的关系？对于直角三角形，三边之间存在怎样的特殊关系？探索勾股定理探索勾股定理做一做 书 P2 ABCABC（图中每个小方格代表一个单位面积）图 1图 2（ 1 ）观察图 1 正方形 A 中含有 个小方格，即 A 的面积是 个单位面积。 正方形 B 的面积是 个单位面积。正方形 C 的面积是 个单位面积。99918你是怎样得到 C 的面积的？与同伴交流交流。123（ 2 ）（ 3 ）探究活动一：ABCABC（图中每个小方格代表一个单位面积）图 1图 2cS正方形143 3182    分割成若干个直角边为整数的三角形（单位面积） 返回ABCABC（图中每个小方格代表一个单位面积）图 1图 2cS正方形216218 （单位面积）把 C 看成边长为 6的正方形面积的一半 返回ABCABC（图中每个小方格代表一个单位面积）图 1图 2（ 2 ）在图 2 中，正方形 A ， B ， C 中各含有多少个小方格？它们的面积各是多少？（ 3 ）你能发现图 1中三个正方形 A ， B ，C 的面积之间有什么关系吗？ SA+SB=SC 即：两条直角边上的正方形面积之和等于 斜边上的正方形的面积 结论 1 以等腰直角三角形两直角边为边长的小正方形的面积的和，等于以斜边为边长的正方形的面积 .探究活动二：ABCCBA（ 1 ）观察右边 两幅图： （ 2 ）填表（每个小正方形的面积为单位 1 ）：A 的面积B 的面积C 的面积左图右图4 916 9？？（ 3 ）你是怎样得到正方形 C 的面积的？与同伴交流 . ABCCBA“ 割”“ 补”“ 拼”（ 4 ）分析填表数据，你发现了什么？ A 的面积B 的面积C 的面积左图4913右图16925CBASSS 结论 2 以直角三角形两直角边为边长的小正方形的面积的和，等于以斜边为边长的正方形的面积 .议一议： （ 1 ）你能用直角三角形的两直角边的长 a 、 b和斜边长 c 来表示图中正方形的面积吗？ ABCCBA（ 2 ）你能发现直角三角形三边长度之间存在什么关系吗？ 结论 3 如果直角三角形两直角边长分别为 a 、 b ，斜边长为 c ，那么即直角三角形两直角边的平方和等于斜边的平方 . 222cbaabcCBA表示为： RtABC△中，∠ C=90° 则222cba 勾股定理（ gou-gu theorem)如果直角三角形两直角边分别为 a 、 b,斜边为 c ，那么222abc即 直角三角形两直角边的平方和等于斜边的平方。abc 在中国古代，人们把弯曲成直角的手臂的上半部分称为...