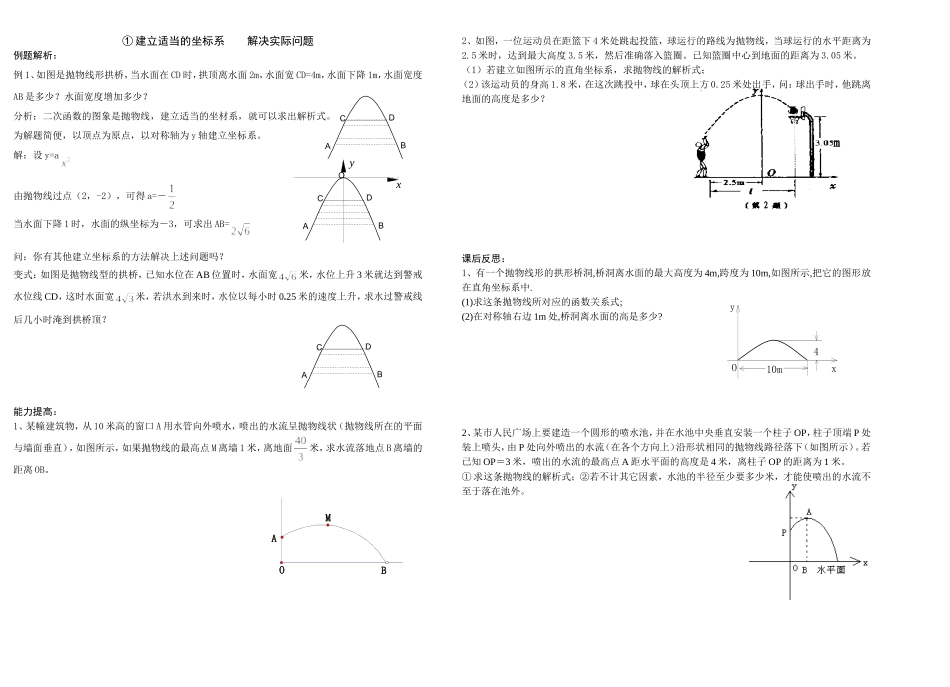
① 建立适当的坐标系 解决实际问题例题解析:例 1、如图是抛物线形拱桥,当水面在 CD 时,拱顶离水面 2m,水面宽 CD=4m,水面下降 1m,水面宽度AB 是多少?水面宽度增加多少?分析:二次函数的图象是抛物线,建立适当的坐材系,就可以求出解析式。为解题简便,以顶点为原点,以对称轴为 y 轴建立坐标系。解:设 y=a由抛物线过点(2,-2),可得 a=-当水面下降 1 时,水面的纵坐标为-3,可求出 AB=问:你有其他建立坐标系的方法解决上述问题吗?变式:如图是抛物线型的拱桥,已知水位在 AB 位置时,水面宽米,水位上升 3 米就达到警戒水位线 CD,这时水面宽米,若洪水到来时,水位以每小时 0.25 米的速度上升,求水过警戒线后几小时淹到拱桥顶?能力提高:1、某幢建筑物,从 10 米高的窗口 A 用水管向外喷水,喷出的水流呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点 M 离墙 1 米,离地面米,求水流落地点 B 离墙的距离 OB。2、如图,一位运动员在距篮下 4 米处跳起投篮,球运行的路线为抛物线,当球运行的水平距离为2.5 米时,达到最大高度 3.5 米,然后准确落入篮圈。已知篮圈中心到地面的距离为 3.05 米。(1)若建立如图所示的直角坐标系,求抛物线的解析式;(2)该运动员的身高 1.8 米,在这次跳投中,球在头顶上方 0.25 米处出手,问:球出手时,他跳离地面的高度是多少?课后反思:1、有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为 4m,跨度为 10m,如图所示,把它的图形放在直角坐标系中.(1)求这条抛物线所对应的函数关系式;(2)在对称轴右边 1m 处,桥洞离水面的高是多少?2、某市人民广场上要建造一个圆形的喷水池,并在水池中央垂直安装一个柱子 OP,柱子顶端 P 处装上喷头,由 P 处向外喷出的水流(在各个方向上)沿形状相同的抛物线路径落下(如图所示)。若已知 OP=3 米,喷出的水流的最高点 A 距水平面的高度是 4 米,离柱子 OP 的距离为 1 米。① 求这条抛物线的解析式;②若不计其它因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外。DCBADCBAAMOB410mxyOm2xyDCBAO