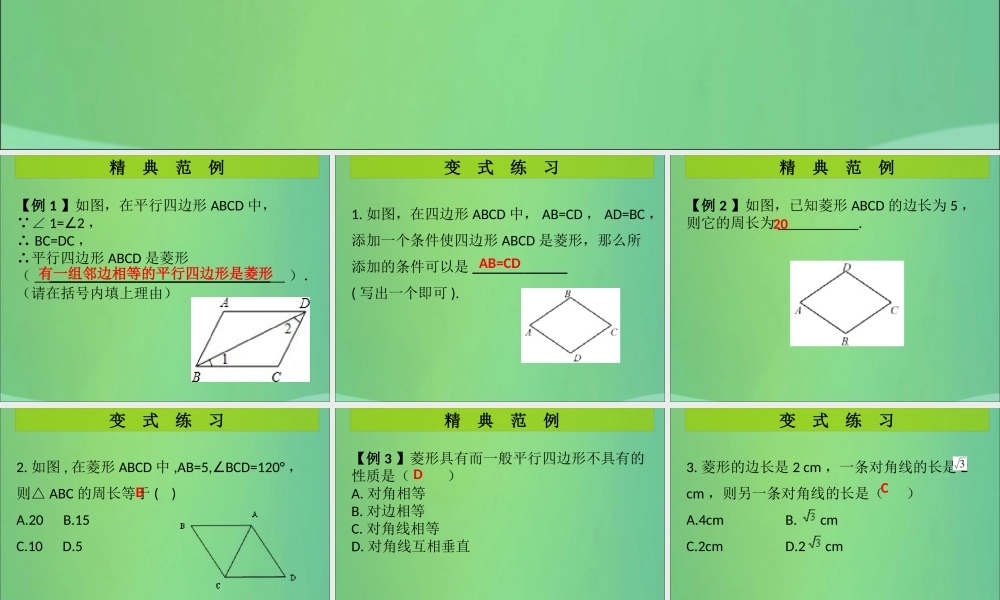
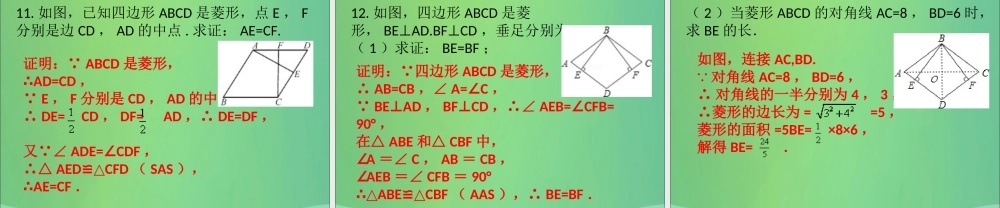
巩固提高精典范例(变式练习)第 1 课时 菱形的性质与判定( 1 )第一章 特殊的平行四边形【例 1 】如图,在平行四边形 ABCD 中, ∠ 1=2∠ ,∴ BC=DC ,∴平行四边形 ABCD 是菱形( __ __ ).(请在括号内填上理由)精 典 范 例有一组邻边相等的平行四边形是菱形1. 如图,在四边形 ABCD 中, AB=CD , AD=BC ,添加一个条件使四边形 ABCD 是菱形,那么所添加的条件可以是 _____________( 写出一个即可 ).变 式 练 习AB=CD【例 2 】如图,已知菱形 ABCD 的边长为 5 ,则它的周长为 ___________.精 典 范 例202. 如图 , 在菱形 ABCD 中 ,AB=5,BCD=120°∠,则△ ABC 的周长等于 ( )A.20 B.15 C.10 D.5 变 式 练 习B【例 3 】菱形具有而一般平行四边形不具有的性质是( )A. 对角相等 B. 对边相等 C. 对角线相等 D. 对角线互相垂直 精 典 范 例D3. 菱形的边长是 2 cm ,一条对角线的长是 2 cm ,则另一条对角线的长是( )A.4cmB. cm C.2cm D.2 cm变 式 练 习C巩 固 提 高4. 菱形的两条对角线分别是 12 cm , 16 cm ,则菱形的边长是( )A.6 cm B.8 cm C.10 cm D.15 cm5. 菱形的周长为 4 ,一个内角为 60° ,则较短的对角线长为( )A.2 B. C.1 D.CC巩 固 提 高6. 如图,在菱形 ABCD 中,∠ ABC=60° , AC=4 ,则 BD 的长为( )A.8 B. 4 C. 2 D.8B巩 固 提 高7. 菱形的边长为 4 ,两邻角度数的比为 1 2∶ ,此菱形的面积为 .8. 已知菱形的边长为 10cm ,两条对角线之比为 3 : 4 ,则菱形两条对角线分别为 .12 cm , 16 cm 巩 固 提 高9. 如图,菱形 ABCD中, AB=4 ,∠ B=60° , AEBC⊥, AFCD⊥,垂足分别为 E , F ,连接 EF ,则△ AEF 的面积是 _______.巩 固 提 高10. 如图,四边形 ABCD 是菱形,对角线 AC 与BD 相交于 O , AB=5 , AO=4.( 1 )求 BD 的长;解:( 1 ) 四边形 ABCD是菱形,对角线 AC 与 BD 相交于 O ,∴ ACBD⊥, DO=BO , AB=5 , AO=4 ,∴BO= =3 ,∴BD=2BO=2×3=6 .巩 固 提 高( 2 )求菱形的面积 .( 2 ) 四边形 ABCD 是菱形,∴AC=2AO=8 ,∴ 菱形 ABCD 的面积 =AC×BD× =24.巩 固 提 高11. 如图,已知四边形 ABCD 是菱形,点 E , F分别...