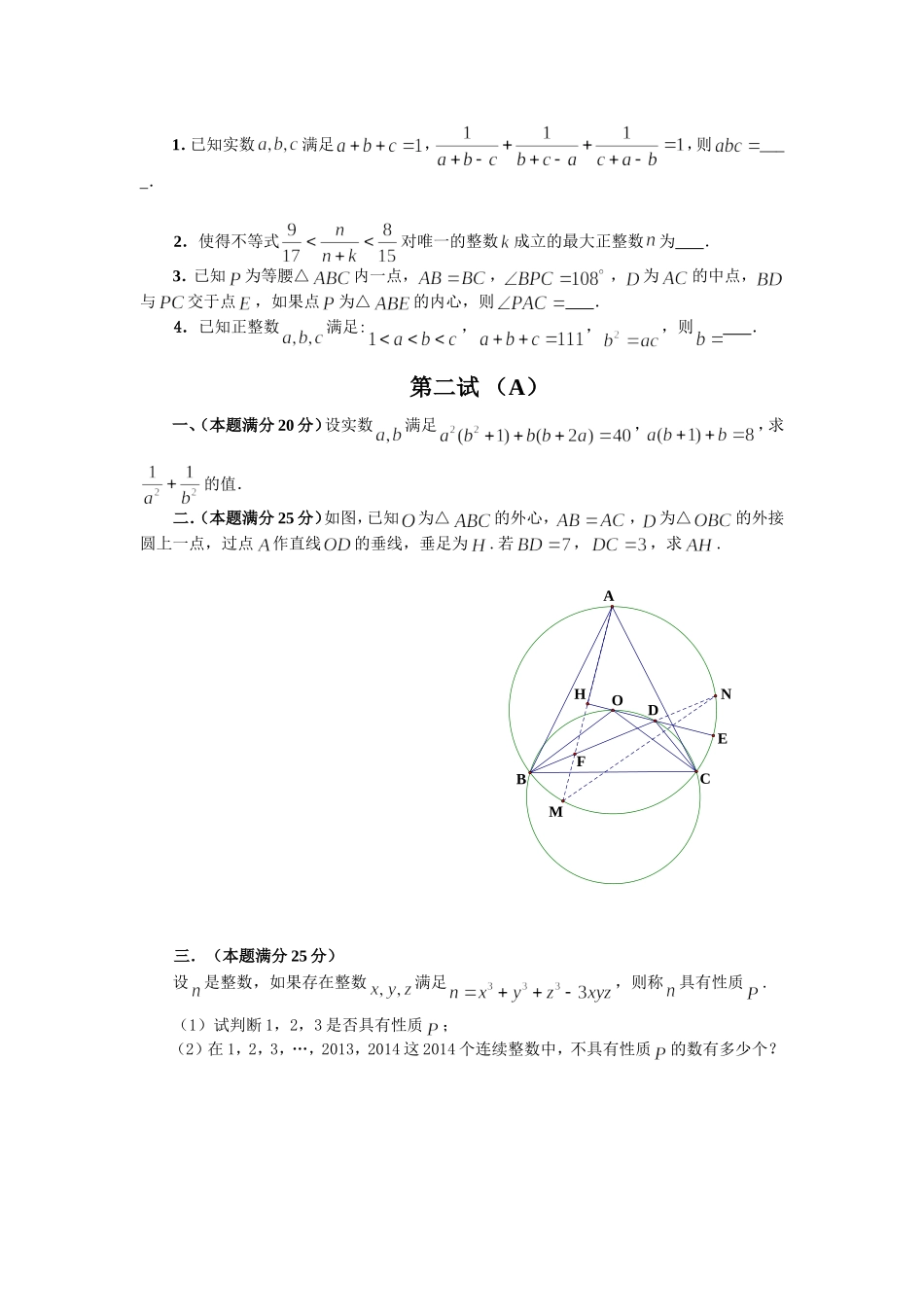
2014 年全国初中数学联合竞赛试题 (3 月 23 日上午 8:30—11:00)第一试得分第二试得分总分计分人考生注意:1.用圆珠笔或钢笔作答. 2.解题书写不要超过装订线.第一试一、选择题(本题满分 42 分,每小题 7 分)本题共有 6 个小题,每题均给出了代号为 A,B,C,D 的四个答案,其中有且仅有一个是正确的.将你所选择的答案的代号填在题后的括号内.每小题选对得 7 分;不选、选错或选出的代号字母超过一个(不论是否写在括号内),一律得 0 分.1.已知为整数,且满足,则的可能的值有( )A. 1 个 B. 2 个 C. 3 个 D. 4 个2.已知非负实数满足,则的最大值为( )A. B. C. D.3.在△中,,为的中点,于,交于,已知,,则= ( )A. B. C. D.4.6 张不同的卡片上分别写有数字 2,2,4,4,6,6,从中取出 3 张,则这 3 张卡片上所写的数字可以作为三角形的三边长的概率是( )A. B. C. D.5.设表示不超过实数 的最大整数,令.已知实数满足,则( )A. B. C. D.16.在△中,,,,在上,在上,使得△为等腰直角三角形, ,则的长为( ) A. B. C. D.二、填空题:(本题满分 28 分,每小题 7 分)得分评卷人1.已知实数满足,,则____.2.使得不等式对唯一的整数成立的最大正整数为 .3.已知为等腰△内一点,,,为的中点,与交于点,如果点为△的内心,则 .4.已知正整数满足:,,,则 .第二试 (A)一、(本题满分 20 分)设实数满足,,求的值.二.(本题满分 25 分)如图,已知为△的外心,,为△的外接圆上一点,过点作直线的垂线,垂足为.若,,求.三.(本题满分 25 分)设是整数,如果存在整数满足,则称具有性质.(1)试判断 1,2,3 是否具有性质;(2)在 1,2,3,…,2013,2014 这 2014 个连续整数中,不具有性质的数有多少个?FMHENAOBCD