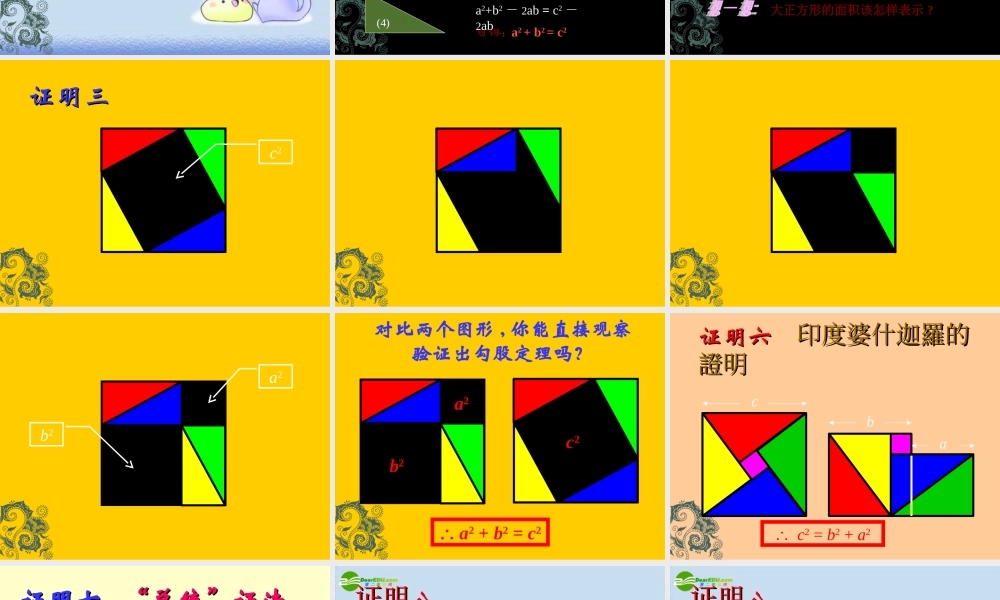
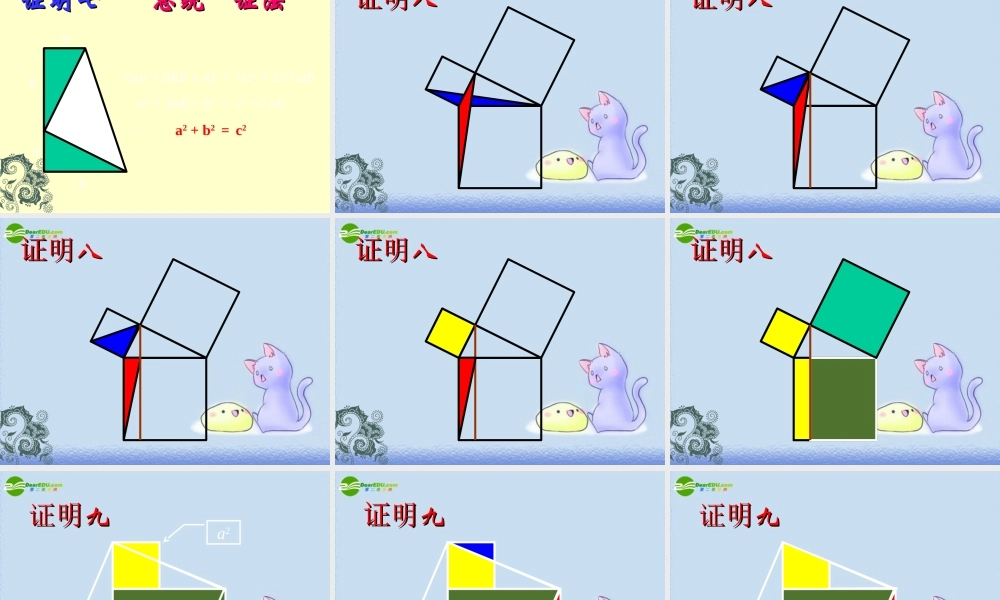
勾股定理的有关证勾股定理的有关证明明勾股定理 :直角三角形两直角边的平方和等于斜边的平方a2+b2=c2b2c2a211美丽的勾股树20022002 年,在北京举行的国际年,在北京举行的国际数学家大会会标数学家大会会标赵爽的“弦图” 早在公元 3 世纪,我国数学家赵爽就用左边的图形验证了“勾股定理”思考 : 你能验证吗?(4)(3)(2)(1)(1)(2)(3)(4)cccc(a-b)2(a-b)2C2 - 4× 21 ab=a2 + b2 = c2可得:a2+b2 - 2ab = c2 -2abbCa想一想:这四个直角三角形还能怎样拼?证明一bababa bacccc大正方形的面积该怎样表示 ?(a+b)2 =a2 + b2 + 2ab = c2+2ab可得 : a2 + b2 = c2ab2142c证明二证明三证明三c2a2b2 a2 + b2 = c2a2b2a2c2对比两个图形 , 你能直接观察验证出勾股定理吗?a证明六证明六 印度婆什迦羅的印度婆什迦羅的證明證明c c2 = b2 + a2b证明七证明七 “总统”证法 “总统”证法 ½(a + b)(b + a) = ½c2 + 2×½ab a2 + 2ab + b2 = c2 +2 ab a2 + b2 = c2aabbcc证证明明八八证证明明八八证证明明八八证证明明八八证证明明八八a2b2证明证明九九证证明明九九证明证明九九证明证明九九证明证明九九c2 a2 + b2 = c2证明九证明九证明九证明九拼拼图游图游戏戏证明九证明九拼图游戏拼图游戏无字证明青出朱方青方朱入朱出青入青入青出青出 abc无字证明无字证明①②③④⑤青出朱入朱出朱方青方青入青入青出青出华罗庚青朱出入图朱入朱出证明证明十十IIIIII注意:面积 I : 面积 II : 面积III= a2 : b2 : c2 IIIIII注意:面积 I : 面积 II : 面积 III= a2 : b2 : c2 证明证明十十IIIIII注意:面积 I : 面积 II : 面积 III= a2 : b2 : c2 证明证明十十注意:面积 I : 面积 II : 面积 III= a2 : b2 : c2 证明证明十十注意:面积 I : 面积 II : 面积 III= a2 : b2 : c2 证明证明十十注意:面积 I : 面积 II : 面积 III= a2 : b2 : c2 证明证明十十注意:面积 I : 面积 II : 面积 III= a2 : b2 : c2 由此得,面积 I + 面积 II = 面积 III因此, a2 + b2 = c2 。证明证明十十 “”在从 面积到乘法公式 一章的学习中,我们把几个图形拼成一个新的图形,通过图形面积的计算得到了许多有用的式子。这节课同样地我们用多种方法拼图验证了勾股定理,你有什么感受? 例 . 在 Rt△ABC 中,∠C =90°. (1) 已知: a=6 ,b =8 ,求 c ; (2) 已知: a=40 , c=41 ,求 b ; (3) 已知: c=13 , b=5 ,求 a ; (4) 已知 : a:b=3:4, c=15, 求 a 、b.例题分析(1) 在直角三角形中 , 已知两边 , 可求第三边 ;(2) 可用勾股定理建立方程 .方法小结3、一个直角三角形的三边长为三个连续偶数 , 则它的三边长分别为 ( )A 2 、 4 、 6C 4 、 6 、 8B试一试 :B 6 、 8 、 10D 8 、 10 、 12