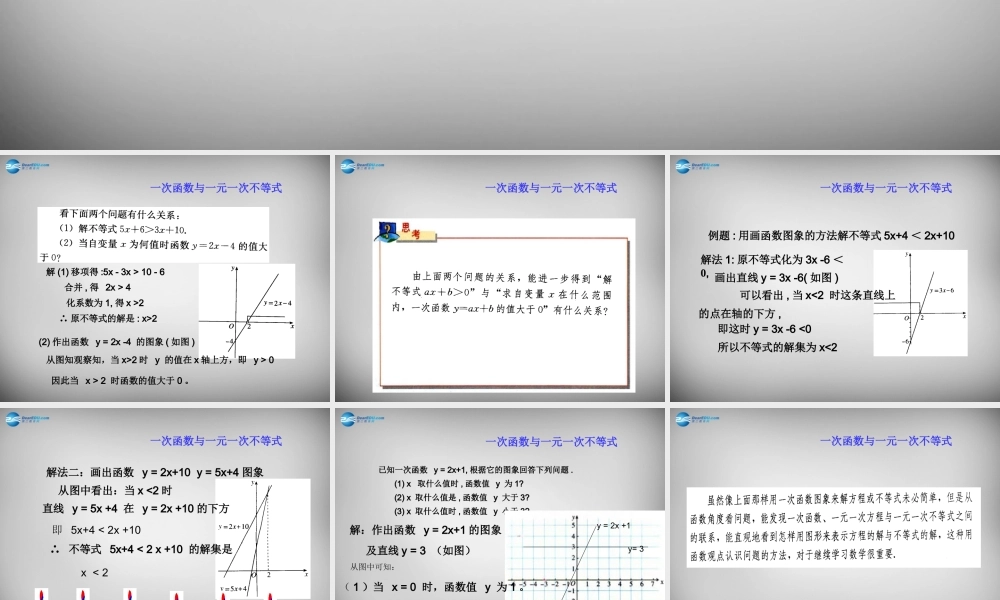
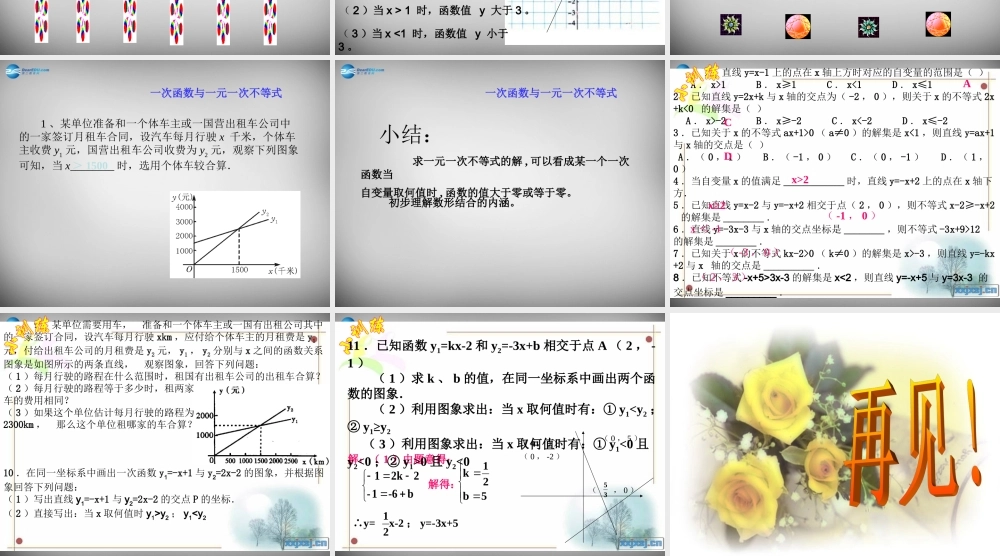
八年级数学解 (1) 移项得 :5x - 3x > 10 - 6合并 , 得 2x > 4∴ 原不等式的解是 : x>2化系数为 1, 得 x >2(2) 作出函数 y = 2x -4 的图象 ( 如图 )从图知观察知,当 x>2 时 y 的值在 x 轴上方,即 y > 0因此当 x > 2 时函数的值大于 0 。一次函数与一元一次不等式一次函数与一元一次不等式例题 : 用画函数图象的方法解不等式 5x+4 < 2x+10解法 1: 原不等式化为 3x -6 <0, 画出直线 y = 3x -6( 如图 ) 可以看出 , 当 x<2 时这条直线上的点在轴的下方 ,即这时 y = 3x -6 <0所以不等式的解集为 x<2一次函数与一元一次不等式解法二:画出函数 y = 2x+10 y = 5x+4 图象 从图中看出:当 x <2 时直线 y = 5x +4 在 y = 2x +10 的下方 即 5x+4 < 2x +10∴ 不等式 5x+4 < 2 x +10 的解集是x < 2一次函数与一元一次不等式已知一次函数 y = 2x+1, 根据它的图象回答下列问题 . (1) x 取什么值时 , 函数值 y 为 1? (2) x 取什么值是 , 函数值 y 大于 3? (3) x 取什么值时 , 函数值 y 小于 3?解:作出函数 y = 2x+1 的图象及直线 y = 3 (如图)y = 2x +1y= 3从图中可知:( 1 )当 x = 0 时,函数值 y 为 1 。( 2 )当 x > 1 时,函数值 y 大于 3 。( 3 )当 x <1 时,函数值 y 小于3 。一次函数与一元一次不等式一次函数与一元一次不等式 1 、某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同,设汽车每月行驶 x 千米,个体车主收费 y1 元,国营出租车公司收费为 y2 元,观察下列图象可知,当 x________ 时,选用个体车较合算.一次函数与一元一次不等式> 1500小结:一次函数与一元一次不等式 求一元一次不等式的解 , 可以看成某一个一次函数当自变量取何值时 , 函数的值大于零或等于零。初步理解数形结合的内涵。 1 .直线 y=x-1 上的点在 x 轴上方时对应的自变量的范围是( ) A . x>1 B . x≥1 C . x<1 D . x≤12 .已知直线 y=2x+k 与 x 轴的交点为( -2 , 0 ),则关于 x 的不等式 2x+k<0 的解集是( ) A . x>-2 B . x≥-2 C . x<-2 D . x≤-23 .已知关于 x 的不等式 ax+1>0 ( a≠0 )的解集是 x<1 ,则直线 y=ax+1与 x 轴的交点是( ) A .( 0...