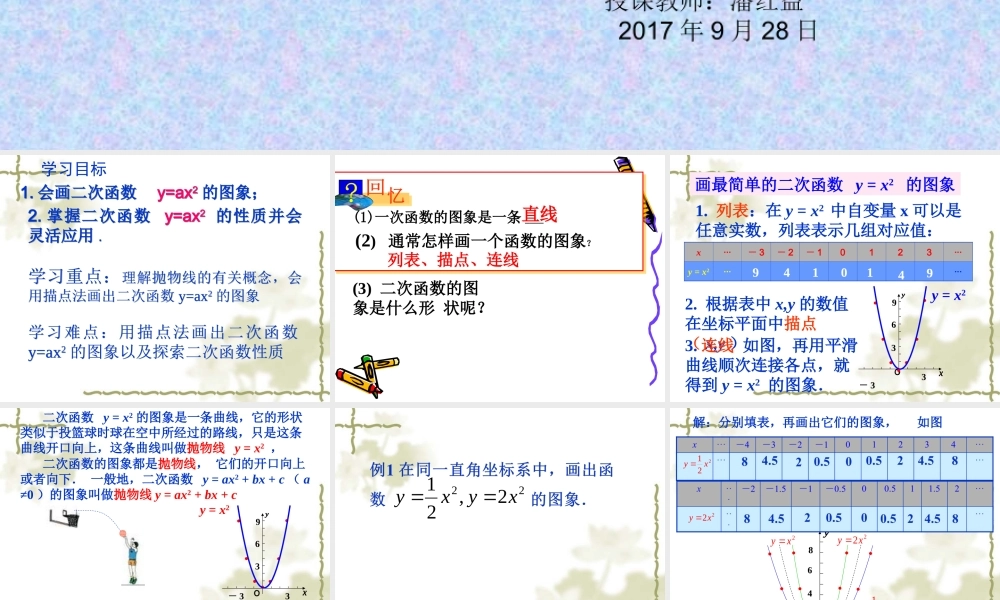
的图象与性质axy2授课教师:潘红益 2017 年 9 月 28 日学习目标1. 会画二次函数 y=ax2 的图象;1. 会画二次函数 y=ax2 的图象;2. 掌握二次函数 y=ax2 的性质并会灵活应用 .学习重点:理解抛物线的有关概念,会用描点法画出二次函数 y=ax2 的图象学习难点:用描点法画出二次函数y=ax2 的图象以及探索二次函数性质2. 掌握二次函数 y=ax2 的性质并会灵活应用 .学习重点:理解抛物线的有关概念,会用描点法画出二次函数 y=ax2 的图象学习难点:用描点法画出二次函数y=ax2 的图象以及探索二次函数性质(1)一次函数的图象是一条 ____ (2) 通常怎样画一个函数的图象?直线(3) 二次函数的图象是什么形 状呢?列表、描点、连线1. 列表:在 y = x2 中自变量 x 可以是任意实数,列表表示几组对应值:x···- 3- 2- 10123···y = x2······2. 根据表中 x,y 的数值在坐标平面中描点( x,y )画最简单的二次函数 y = x2 的图象 - 3336901491493. 连线 如图,再用平滑曲线顺次连接各点,就得到 y = x2 的图象.y = x2 二次函数 y = x2 的图象是一条曲线,它的形状类似于投篮球时球在空中所经过的路线,只是这条曲线开口向上,这条曲线叫做抛物线 y = x2 , 看出: y 轴是抛物线 y = x 2 的对称轴,抛物线 y = x 2 与它的对称轴的交点( 0 , 0 )叫做抛物线 y = x2 的顶点,它是抛物线 y = x 2 的最低点.- 33369 二次函数的图象都是抛物线, 它们的开口向上或者向下. 一般地,二次函数 y = ax2 + bx + c ( a≠0 )的图象叫做抛物线 y = ax2 + bx + c 实际上,每条抛物线都有对称轴,抛物线与对称轴的交点叫做抛物线的顶点.顶点是抛物线的最低点或最高点.y = x2222,21xyxy解:分别填表,再画出它们的图象, 如图 - 222464- 48212yx22yx2yx212yx22yx函数 的图象与函数 y=x2 的图象相比,有什么共同点和不同点?222,21xyxy - 2 2246 4 - 48212yx22yx2yx相同点:开口:向上, 顶点:原点( 0,0 )——最低点 对称轴: y 轴增减性: y 轴左侧, y 随 x 增大而减小 y 轴右侧, y 随 x 增大而增大也就是说: x < 0 时, y 随 x 的增大而减少 x > 0 时, y 随 x 的增大而增大不同点: a 值越大,抛物线的开口越小.探究 画出函数 的图...