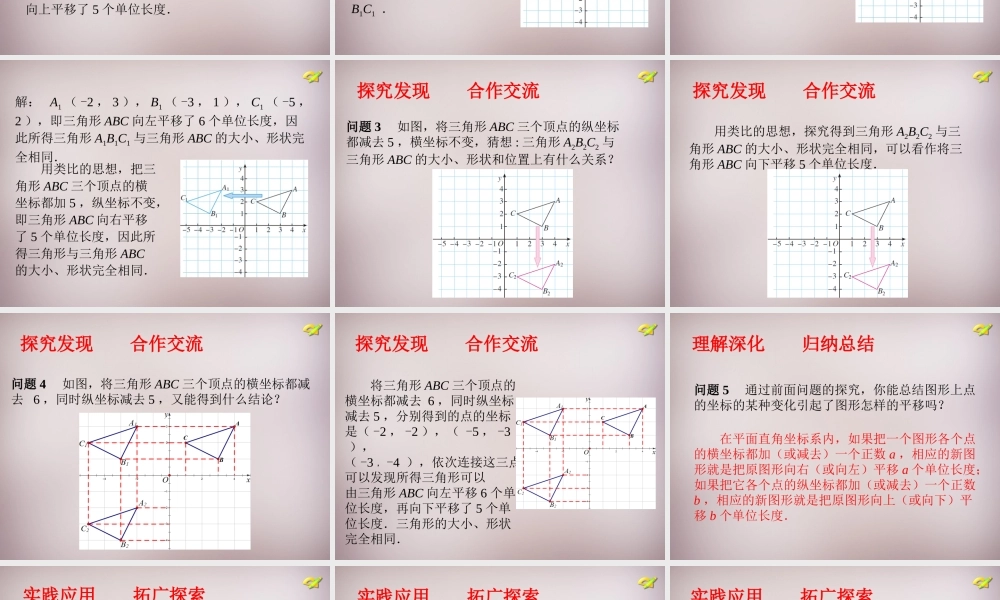
7.2 坐标方法的简单应用(第 3 课时) 上一节课学习了图形的平移引起的图形上的点的坐标的变化规律,反过来,这节课探讨图形上点的坐标的某种变化引起的图形平移.课件说明学习目标:会根据图形上点的坐标的某种变化,得出图形进行了怎样的平移.学习重点:在平面直角坐标系中,探究点的坐标的某种变化引起的图形平移.课件说明问题 1 如图,已知点 A 的坐标是( -2 , -3 ),把它的横坐标加 5 ,纵坐标不变,得到点 A1 ,点 A1的坐标是什么?点 A 所在位置发生了什么变化?若点 A 的横坐标不变,纵坐标加 4 呢? 设置问题 引出新课A2A1A问题 1 已知点 A 的坐标是( -2 , -3 ),把它的横坐标加 5 ,纵坐标不变,得到点 A1 的坐标是 (3 , -3) ,即点 A 向右平移了 5 个单位长度;若点 A 的横坐标不变,纵坐标加 4 ,得到点 A2 的坐标是 ( -2 , 1 ),即点 A向上平移了 5 个单位长度.设置问题 引出新课A2A1A( 1 )将三角形 ABC 三个顶点的横坐标都减去 6 ,纵坐标不变,分别得到点 A1 , B1 , C1 ,点 A1 , B1 , C1 坐标分别是什么?并画出相应的三角形 A1B1C1 .探究发现 合作交流问题 2 如图,三角形 ABC 三个顶点的坐标分别是: A ( 4 , 3 ), B ( 3 , 1 ), C ( 1 ,2 ).( 2 )三角形 A1B1C1 与三角形 ABC 的大小、形状和位置上有什么关系,为什么?( 3 )若三角形 ABC 三个顶点的横坐标都加 5 ,纵坐标不变呢?探究发现 合作交流问题 2 如图,三角形 ABC 三个顶点的坐标分别是: A ( 4 , 3 ), B ( 3 , 1 ), C ( 1 ,2 ).解: A1 ( -2 , 3 ), B1 ( -3 , 1 ), C1 ( -5 ,2 ),即三角形 ABC 向左平移了 6 个单位长度,因此所得三角形 A1B1C1 与三角形 ABC 的大小、形状完全相同. 用类比的思想,把三角形 ABC 三个顶点的横坐标都加 5 ,纵坐标不变,即三角形 ABC 向右平移了 5 个单位长度,因此所得三角形与三角形 ABC的大小、形状完全相同.问题 3 如图,将三角形 ABC 三个顶点的纵坐标都减去 5 ,横坐标不变,猜想 : 三角形 A2B2C2 与三角形 ABC 的大小、形状和位置上有什么关系?探究发现 合作交流 用类比的思想,探究得到三角形 A2B2C2 与三角形 ABC 的大小、形状完全相同,可以看作将三角形 A...