数学：221(双曲线及其标准方程)PPT课件(新人教A版-选修1-1) 课件VIP免费

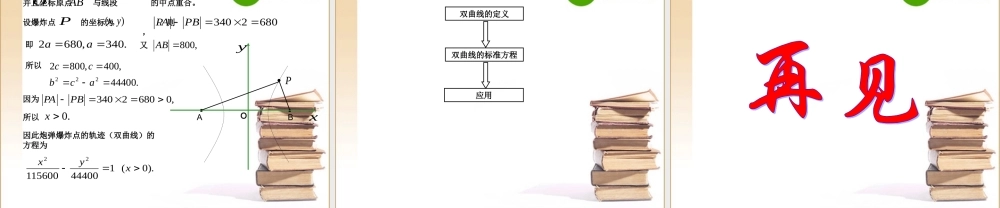
2.2.1 《双曲线及其标准方程》 教学目标 • 知识与技能目标• 理解双曲线的概念，掌握双曲线的定义、会用双曲线的定义解决实际问题；理解双曲线标准方程的推导过程及化简无理方程的常用的方法；了解借助信息技术探究动点轨迹的《几何画板》的制作或操作方法。。• 过程与方法目标过程与方法目标• （（ 11 ）预习与引入过程）预习与引入过程• 预习教科书有关内容，思考当变化的平面与圆锥轴预习教科书有关内容，思考当变化的平面与圆锥轴所成的角在变化时，观察平面截圆锥的截口曲线（所成的角在变化时，观察平面截圆锥的截口曲线（截面与圆锥侧面的交线）是什么图形？又是怎么样截面与圆锥侧面的交线）是什么图形？又是怎么样变化的？变化的？ 问题 1 ：椭圆的定义是什么？平面内与两个定点 的距离的和等于常数（大于 ）的点的轨迹叫做椭圆。21, FF21FF问题 2 ：椭圆的标准方程是怎样的 ?)0(1)0(122222222babxaybabyax或 ， ， 关系如何？a bc222cba问题 3 ：如果把上述定义中“距离的和”改为“距离的差”那么点 的轨迹会发生怎样的变化？1. 双曲线的定义：平面内与两个定点 的距离的差的绝对值等于常数（小于 ）的点的轨迹叫做双曲线。21, FF21FF这两个定点叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距。1F2FM常数21MFMF2. 标准方程的推导① 建系1F2F使 轴经过两焦点 ， 轴为线段 的垂直平分线。x21,FF21,FFyxyO② 设点设 是双曲线上任一点，),(yxMM焦距为 ，那么 焦点 又设点 与 的差的绝对值等于常数 。)0(2cc)0,(),0,(21cFcF M21, FFa2③ 列式aMFMF221即aycxycx2)()(2222④ 化简两边同除以 得)(222aca122222acyax)()(22222222acayaxac得02222acacac)0(222bbac令代入得)0,0(12222babyax这个方程叫做双曲线的标准方程。它所表示的是焦点在 轴上 x)0,(),0,(21cFcF .222bac焦点在 轴上的双曲线的标准方程是什么？y1F2FxyO)0,0(12222babxay)0,0(12222babxay)0,0(12222babyax3. 两种标准方程的比较① 方程用“－”号连接。② 分母是 但 大小不定。0,0,,22bababa,③ 。 222bac④ 如果 的系数是正的，则焦点在 轴上；如果 的系数是正的，则焦点在 轴上。2xx2yy判断下列方程是否表示双曲线？若是，求出 及焦点坐标。cba,,  ...