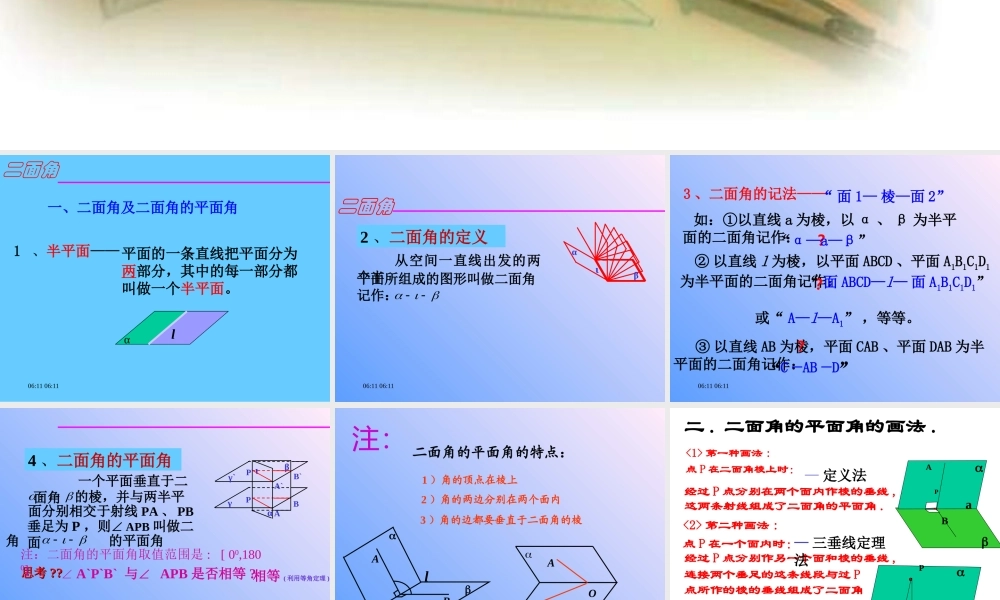
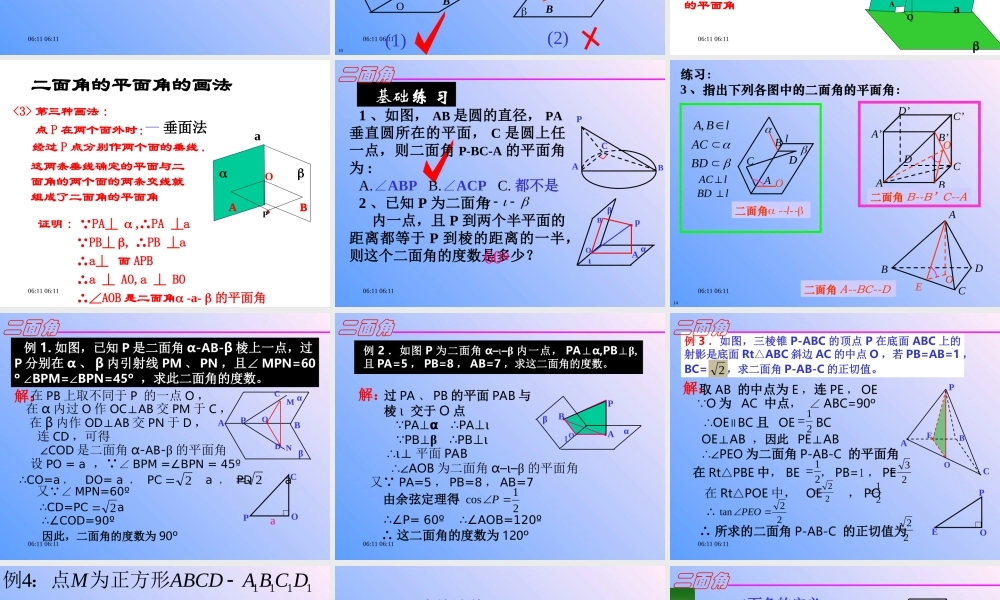
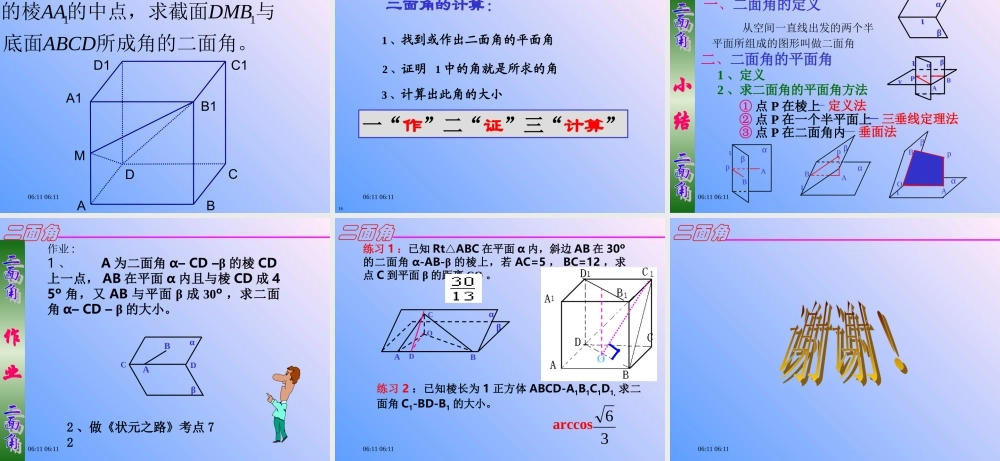
06:11 06:11 二面角06:11 06:11 一、二面角及二面角的平面角平面的一条直线把平面分为两部分,其中的每一部分都叫做一个半平面。1 、半平面——αlαl二面角06:11 06:11 从空间一直线出发的两个半2 、二面角的定义αβι平面所组成的图形叫做二面角记作:二面角二面角06:11 06:11 3 、二面角的记法——“ 面 1— 棱—面 2” ③ 以直线 AB 为棱,平面 CAB 、平面 DAB 为半平面的二面角记作: ② 以直线 l 为棱,以平面 ABCD 、平面 A1B1C1D1为半平面的二面角记作:或“ A—l—A1” ,等等。?“α—a—β”?“ 面 ABCD—l— 面 A1B1C1D1”?“C—AB—D” 如:①以直线 a 为棱,以 α 、 β 为半平面的二面角记作:06:11 06:11 4 、二面角的平面角角 的平面角 一个平面垂直于二面角 的棱,并与两半平面分别相交于射线 PA 、 PB垂足为 P ,则∠ APB 叫做二面ABPγβαιA`B`P`γ`∠ A`P`B` 与∠ APB 是否相等 ?思考思考 ????相等 ( 利用等角定理 )注:二面角的平面角取值范围是 : [ 00,1800]06:11 06:11 注: 二面角的平面角的特点:3 )角的边都要垂直于二面角的棱1 )角的顶点在棱上2 )角的两边分别在两个面内10lOABAOB(1)(2)06:11 06:11 二 . 二面角的平面角的画法 . <1> 第一种画法 : 点 P 在二面角棱上时: <2> 第二种画法 : 点 P 在一个面内时: a a 经过 P 点分别在两个面内作棱的垂线 , 这两条射线组成了二面角的平面角 .经过 P 点分别作另一个面和棱的垂线 ,连接两个垂足的这条线段与过 P点所作的棱的垂线组成了二面角的平面角 P P A B A O — 定义法— 三垂线定理法06:11 06:11 二面角的平面角的画法 <3> 第三种画法 : 点 P 在两个面外时: 这两条垂线确定的平面与二面角的两个面的两条交线就组成了二面角的平面角 O A B a P 经过 P 点分别作两个面的垂线 . A B 证明 : PA⊥ ,∴PA ⊥a PB⊥ , ∴PB ⊥a ∴a⊥ 面 APB ∴a ⊥ AO,a ⊥ BO ∴∠AOB 是二面角 -a- 的平面角— 垂面法06:11 06:11 1 、如图, AB 是圆的直径, PA垂直圆所在的平面, C 是圆上任一点,则二面角 P-BC-A 的平面角为 :A.ABP∠ B.ACP∠ C. 都不是 基础练 习2 、已知 P 为二面角 内一点,且 P ...