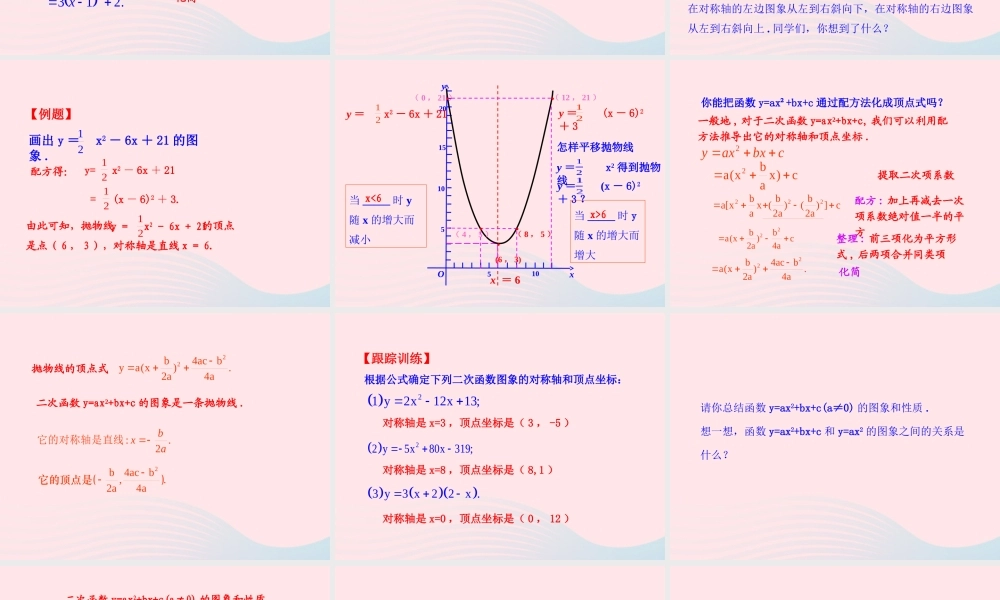
26.1.4 二次函数 y=ax2+bx+c 的图象1. 会画 y=ax2+bx+c 的图象;2. 理解 y=ax2+bx+c 的性质;3. 掌握 y=ax2+bx+c 与 y=a(x-h)2+k 的图象及性质的联系与区别 . 说出二次函数的图象的开口方向、对称轴、顶点坐标 . 它是由 y=-4x2 怎样平移得到的?1)2(42 xy怎样直接作出函数 y=3x2-6x+5 的图象 ?配方化成顶点式我们知道 , 作出二次函数 y=3x2 的图象 , 通过平移抛物线 y=3x2 可以得到二次函数 y=3x2-6x+5 的图象 . 5632xxy23(x2x)5提取二次项系数23(x2x 1 1)5 配方 : 加上再减去一次项系数绝对值一半的平方23 x135整理 : 前三项化为完全平方式 , 后两项合并同类项.2132 x化简x… -2-101234… … 29145251429…2y3(x 1)2列表 : 根据对称性 , 选取适当值列表计算 . a=3>0,∴ 开口向上 ; 对称轴 : 直线 x=1; 顶点坐标 :(1,2).再根据顶点式确定开口方向、对称轴、顶点坐标 .x=1● (1 , 2)5632xxy通过图象你能看出当 x 取何值时 y 随x 的增大而减小,当 x 取何值时, y随 x 的增大而增大吗?当 x<1 时 y 随 x 的增大而减小 ; 当 x>1 时,y 随 x 的增大而增大 .在对称轴的左边图象从左到右斜向下,在对称轴的右边图象从左到右斜向上 . 同学们,你想到了什么?0画出 y = x2 - 6x + 21 的图象 .21配方得:y= x2 - 6x + 2121= (x - 6)2 + 3.由此可知,抛物线 的顶点是点( 6 , 3 ),对称轴是直线 x = 6.y = x2 - 6x + 212121【例题】Oyx5105102015x = 6y = (x - 6)2+ 321y = x2 - 6x + 2121怎样平移抛物线y = x2 得到抛物线y = (x - 6)2+ 3 ?当 _____ 时 y随 x 的增大而增大当 _____ 时 y随 x 的增大而减小x>6x<6·( 8 , 5 )·( 4 , 5 )· (6 , 3)·( 12 , 21 )·( 0 , 21 )cbxaxy22ba(xx)ca提取二次项系数222bbba[xx ()() ]ca2a2a配方 : 加上再减去一次项系数绝对值一半的平方22bba(x)c2a4a整理 : 前三项化为平方形式 , 后两项合并同类项22b4acba(x).2a4a化简一般地 , 对于二次函数 y=ax²+bx+c, 我们可以利用配方法推导出它的对称轴和顶点坐标 . 你能把函数 y=ax²+bx+c 通过配方法化成顶点式吗?...