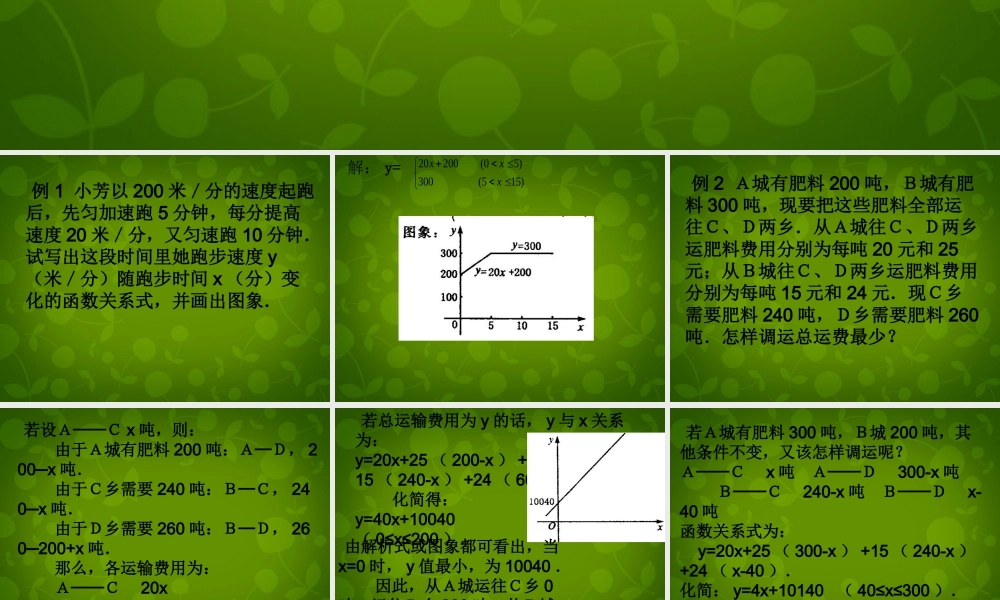
11 . 2 . 2 一次函数 ( 三 ) 例 1 小芳以 200 米/分的速度起跑后,先匀加速跑 5 分钟,每分提高速度 20 米/分,又匀速跑 10 分钟.试写出这段时间里她跑步速度 y(米/分)随跑步时间 x (分)变化的函数关系式,并画出图象. 解: y=20200(05)300(515)xxx 例 2 A城有肥料 200 吨,B城有肥料 300 吨,现要把这些肥料全部运往C、D两乡.从A城往C、D两乡运肥料费用分别为每吨 20 元和 25元;从B城往C、D两乡运肥料费用分别为每吨 15 元和 24 元.现C乡需要肥料 240 吨,D乡需要肥料 260吨.怎样调运总运费最少? 若设A──C x 吨,则: 由于A城有肥料 200 吨:A─D, 200─x 吨. 由于C乡需要 240 吨:B─C, 240─x 吨. 由于D乡需要 260 吨:B─D, 260─200+x 吨. 那么,各运输费用为: A──C 20x A──D 25 ( 200-x ) B──C 15 ( 240-x )B──D 24 ( 60+x ) 若总运输费用为 y 的话, y 与 x 关系为:y=20x+25 ( 200-x ) +15 ( 240-x ) +24 ( 60+x ). 化简得:y=40x+10040 ( 0≤x≤200 ). 由解析式或图象都可看出,当x=0 时, y 值最小,为 10040 . 因此,从A城运往C乡 0吨,运往D乡 200 吨;从B城运往C乡 240 吨, 运往D乡 60 吨.此时总运费最少,为 10040 元. 若A城有肥料 300 吨,B城 200 吨,其他条件不变,又该怎样调运呢?A──C x 吨 A──D 300-x 吨 B──C 240-x 吨 B──D x-40 吨函数关系式为: y=20x+25 ( 300-x ) +15 ( 240-x )+24 ( x-40 ). 化简: y=4x+10140 ( 40≤x≤300 ). 由解析式可知:当 x=40 时 y 值最小为 y=4×40+10140=10300 因此从A城运往C乡 40 吨,运往D乡 260 吨;从B城运往C乡 200 吨,运往D乡 0 吨.此时总运费最小值为10300 吨.练习 从A、B两水库向甲、乙两地调水,其中甲地需水 15 万吨,乙地需水 13 万吨,A、B两水库各可调出水 14 万吨.从A地到甲地50 千米,到乙地 30 千米;从B地到甲地 60 千米,到乙地 45 千米.设计一个调运方案使水的调运量(万吨 · 千米)最少. 解答:设总调运量为 y 万吨 · 千米,A水库调往甲地水 x 万吨,则调往乙地( 14-x )万吨,B水库调往甲地水( 15-x )万吨,调往乙地水( x-1 )万吨. 由调运量与各距离的关系,可知反映 y 与 x 之间的函数为: y=50x+30 ( 14-x ) +60 ( 15-x ) +45 ( x-1 ). 化简得: y=5x+1275 ( 1≤x≤14 ). 由解析式可知:当 x=1 时, y 值最小,为 y=5×1+1275=1280 . 因此从A水库调往甲地 1 万吨水,调往乙地 13万吨水;从B水库调往甲地 14 万吨水,调往乙地 0万吨水.此时调运量最小,调运量为 1280 万吨 · 千米.