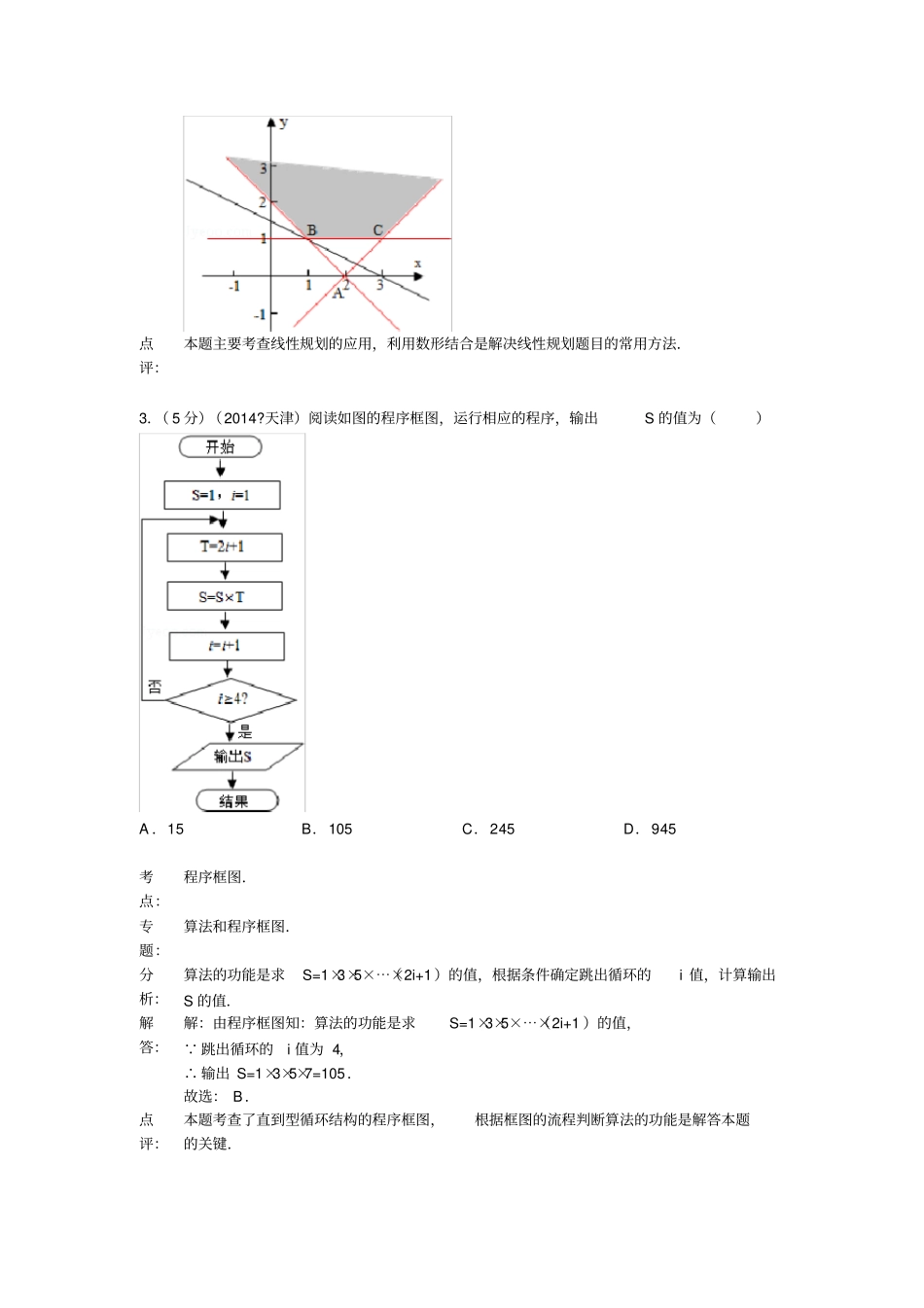
2014 年天津市高考数学试卷(理科)参考答案与试题解析一、选择题(共8 小题,每小题5 分)1.( 5 分)(2014?天津) i 是虚数单位,复数=()A .1﹣i B.﹣1+i C.+i D.﹣+i 考点:复数代数形式的乘除运算.专题:数系的扩充和复数.分析:将复数的分子与分母同时乘以分母的共轭复数3﹣4i,即求出值.解答:解:复数==,故选 A.点评:本题考查了复数的运算法则和共轭复数的意义,属于基础题.2.( 5 分)(2014?天津)设变量x,y 满足约束条件,则目标函数z=x+2y 的最小值为()A .2B.3C.4D.5考点:简单线性规划.专题:不等式的解法及应用.分析:作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求z 的最大值.解答:解:作出不等式对应的平面区域,由 z=x+2y ,得 y=﹣,平移直线 y= ﹣,由图象可知当直线y= ﹣经过点 B( 1,1)时,直线y=﹣的截距最小,此时z 最小.此时 z 的最小值为z=1+2 ×1=3,故选: B.点评:本题主要考查线性规划的应用,利用数形结合是解决线性规划题目的常用方法.3.( 5 分)(2014?天津)阅读如图的程序框图,运行相应的程序,输出S 的值为()A .15 B.105 C.245 D.945 考点:程序框图.专题:算法和程序框图.分析:算法的功能是求S=1×3×5×⋯×(2i+1)的值,根据条件确定跳出循环的i 值,计算输出S 的值.解答:解:由程序框图知:算法的功能是求S=1×3×5×⋯×(2i+1 )的值, 跳出循环的i 值为 4,∴ 输出 S=1×3×5×7=105.故选: B.点评:本题考查了直到型循环结构的程序框图,根据框图的流程判断算法的功能是解答本题的关键.4.( 5 分)(2014?天津)函数f(x)=log(x2﹣4)的单调递增区间为()A .(0,+∞)B.(﹣∞,0)C.(2,+∞)D.(﹣∞,﹣ 2)考点:复合函数的单调性.专题:函数的性质及应用.分析:令 t=x2﹣4>0,求得函数f(x)的定义域为(﹣∞,﹣ 2)∪(2,+∞),且函数 f( x)=g( t)=logt.根据复合函数的单调性,本题即求函数t 在(﹣ ∞,﹣2)∪(2,+∞)上的减区间.再利用二次函数的性质可得,函数t 在(﹣ ∞,﹣ 2)∪(2,+∞) 上的减区间.解答:解:令 t=x 2﹣4>0,可得x>2,或 x<﹣ 2,故函数 f (x)的定义域为(﹣∞,﹣ 2)∪ (2,+∞),当 x∈(﹣ ∞,﹣ 2)时, t 随 x 的增大而减小,y=logt 随 t 的减小而增大,所以 y=lo...