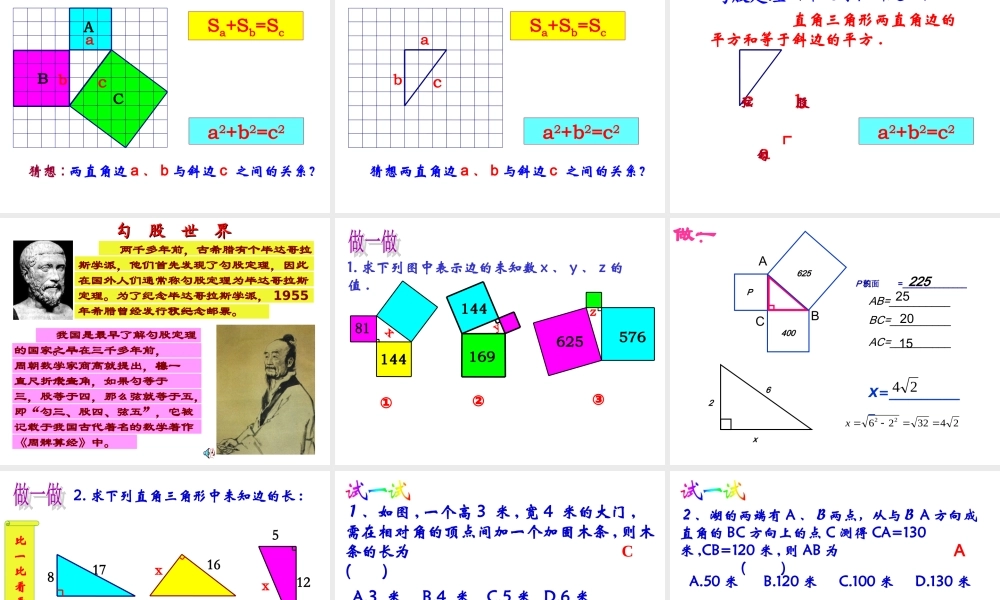
人教版八年级(下)第十八章 北京欢迎您! 读一读 我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦 . 图 1-1 称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的 . 图 1-2 是在北京召开的 2002 年国际数学家大会( TCM - 2002 )的会标,其图案正是“弦图”,它标志着中国古代的数学成就 . 图 1-1图 1-2 勾股定理( 1 )看一看 相传2500年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?ABCABC(图中每个小方格代表一个单位面积)图 2-1图 2-2( 1 )观察图2-1 正方形 A 中含有 个小方格,即 A 的面积是 个单位面积。 正方形 B 的面积是 个单位面积。正方形 C 的面积是 个单位面积。99918你是怎样得到上面的结果的?与同伴交流交流。ABCABC(图中每个小方格代表一个单位面积)图 2-1图 2-2cS正方形143 3182 分“割”成若干个直角边为整数的三角形(单位面积)ABCABC(图中每个小方格代表一个单位面积)图 2-1图 2-2cS正方形216218 (单位面积)把 C“ 补” 成边长为 6的正方形面积的一半ABCABC(图中每个小方格代表一个单位面积)图 2-1图 2-2( 2 )在图 2-2 中,正方形 A , B , C中各含有多少个小方格?它们的面积各是多少?( 3 )你能发现图2-1 中三个正方形A , B , C 的面积之间有什么关系吗? SA+SB=SC 即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积ABC图 3-1ABC图 3-2分割成若干个直角边为整数的三角形cS正方形25144 3 12 (面积单位)一般的直角三角形三边为边作正方形ABC图 3-1ABC图 3-2把 C“ 补”成边长为 7的正方形面积加1 单位面积的一半cS正方形25(面积单位)思考:面积A , B , C 还有上述关系吗?)(17212 ABC图 3-1ABC图 3-2( 1 )你能用三角形的边长表示正方形的面积吗?( 2 )你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流。议一议 ABCacbSa+Sb=Sc 观察所得到的各组数据,你有什么发现?猜想 : 两直角边 a 、 b 与斜边 c 之间的关系?a2+b2=c2acb 观察所得到的各组数据,你有什么发现?猜想两直角边 a 、 b 与斜边 c 之间的关系?a2+b2=c2Sa+Sb=Sc┏a2+...