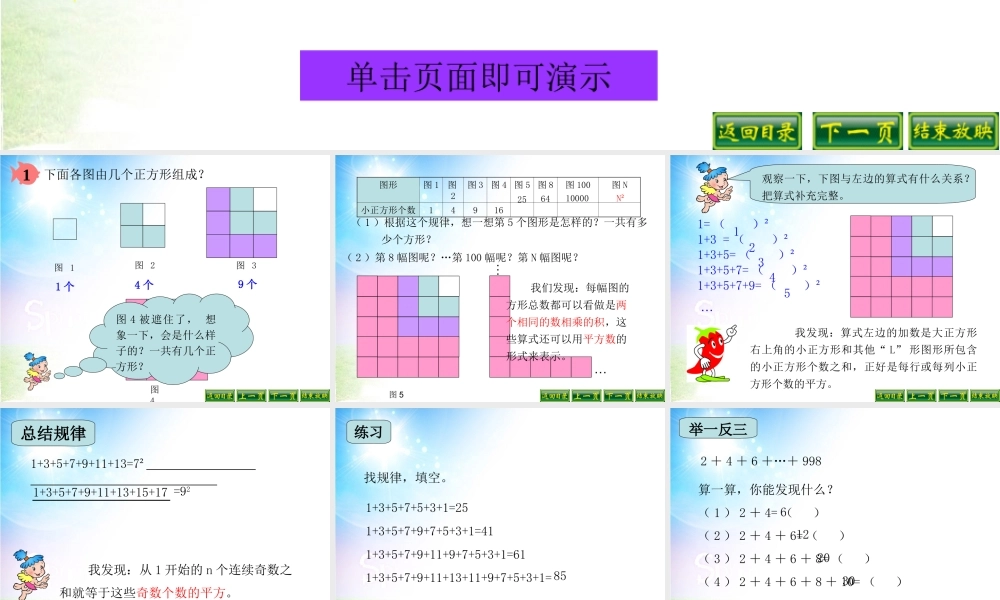
人教版数学六年级 ( 上册 )单击页面即可演示图 1图 2图 3图 4 被遮住了, 想象一下,会是什么样子的?一共有几个正方形? 1 个4 个9 个图 41下面各图由几个正方形组成?( 1 )根据这个规律,想一想第 5 个图形是怎样的?一共有多 少个方形?( 2 )第 8 幅图呢?…第 100 幅呢?第 N 幅图呢?图形图 1图2图 3图 4图 5图 8图 100图 N小正方形个数1491625图 5……6410000N² 我们发现:每幅图的方形总数都可以看做是两个相同的数相乘的积,这些算式还可以用平方数的形式来表示。 1= ( )² 1+3 = ( )² 1+3+5= ( )² 1+3+5+7= ( )² 1+3+5+7+9= ( )² 观察一下,下图与左边的算式有什么关系?把算式补充完整。…12345 我发现:算式左边的加数是大正方形右上角的小正方形和其他“ L” 形图形所包含的小正方形个数之和,正好是每行或每列小正方形个数的平方。总结规律1+3+5+7+9+11+13=7² 我发现:从 1 开始的 n 个连续奇数之和就等于这些奇数个数的平方。 1+3+5+7+9+11+13+15+17 =921+3+5+7+5+3+1=251+3+5+7+9+7+5+3+1=411+3+5+7+9+11+9+7+5+3+1=611+3+5+7+9+11+13+11+9+7+5+3+1=练习85找规律,填空。举一反三2 + 4 + 6 +…+ 998 算一算,你能发现什么?( 1 ) 2 + 4= ( )( 2 ) 2 + 4 + 6= ( )( 3 ) 2 + 4 + 6 + 8= ( )( 4 ) 2 + 4 + 6 + 8 + 10= ( ) …6122030( 1 ) 2 + 4= ( ) × ( ) = ( )²+( )( 2 ) 2 + 4 + 6= ( ) × ( ) = ( )²+( )( 3 ) 2 + 4 + 6 + 8= ( ) × ( ) = ( )²+( )画一画、分一分、填一填232234334544 从 2 起连续偶数的和等于偶数个数的平方加偶数个数,即 ,或等于偶数个数乘比偶数个数大 1 的数,即 。(用 n 表示偶数个数)2 + 4 + 6 +…+998 你发现了什么?n²+nn×(n +1)( 2 )你能解释其中的道理吗? 红色1234……蓝色8101214 ( 1 )照这样接着画下去,第 5 个图形有多少个红色小正方形和多少个蓝色小正方形?第 10 个图形呢?巩固练习15161026每增加一个红色小正方形就会增加两个蓝色小正方形。3²-1=85²-3² =167²-5² =24 照这样接着画下去,第 5 个图形最外圈有多少个小正方形?巩固练习 24011112113311464115101051仔细观察图表,同桌互相分享各自的发现。 你能按照发现的规律继续写下去吗?1615201561 这样的由数构成的图表早在我国南宋数学家 杨 辉 1261 年 所 著 的《详解九章算法》一书里就已经出现了,在这本书里,记载着类似的表,我们把它称为“杨辉三角”。 你知道吗?