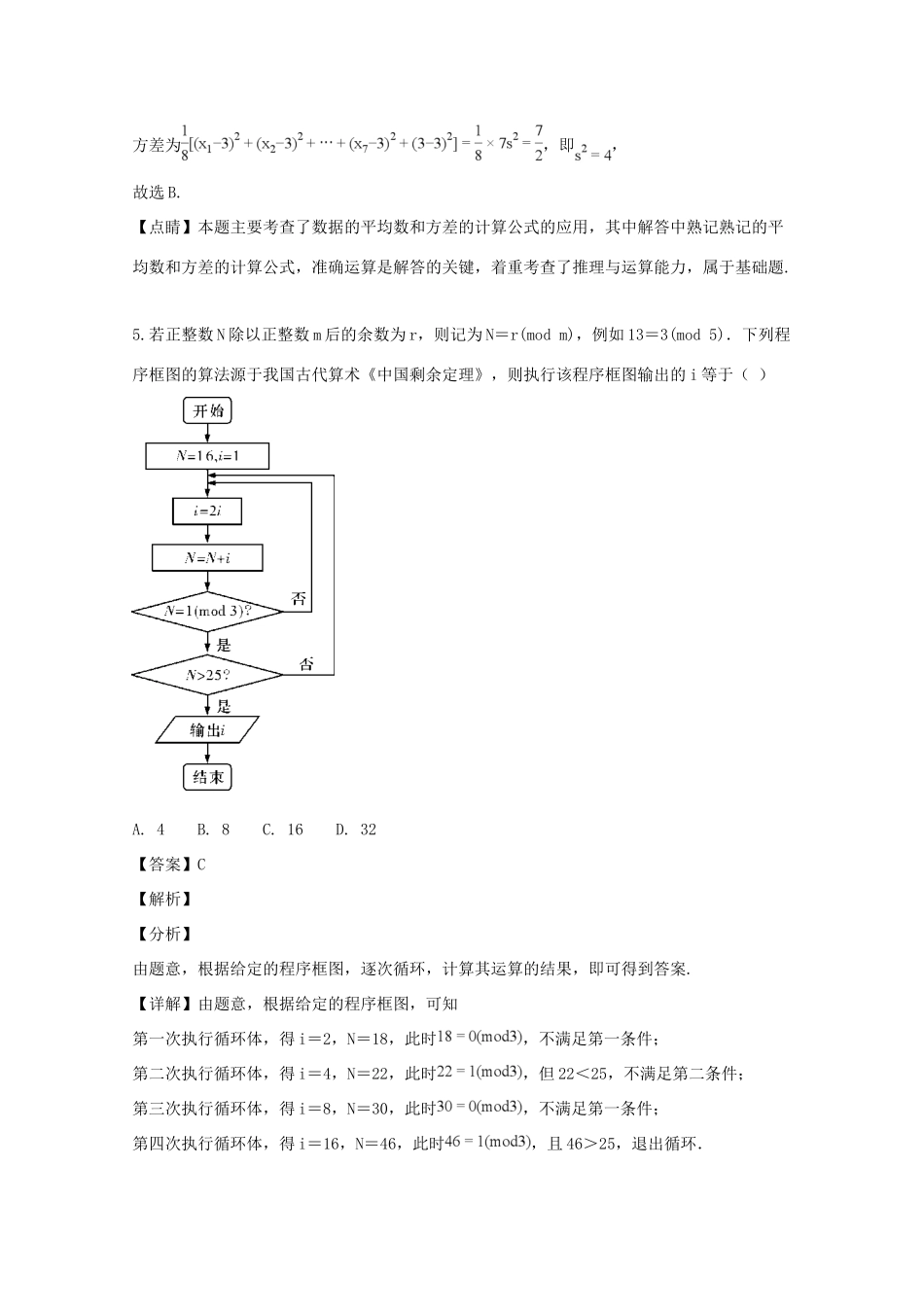
湖南师大附中 2019 届高三月考试卷(五)数学(理科)一、选择题:本大题共 12 小题,每小题 5 分,共 60 分,在每小题的四个选项中,只有一项是符合题目要求的.1.若复数 z 满足 (i 为虚数单位),则 z 在复平面内对应的点位于( )A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限【答案】D【解析】【分析】由题意,根据复数的运算,化简求得,则 z 对应的点为(2,-1),即可得到答案.【详解】由题意,复数,则 z 对应的点为(2,-1).故选D.【点睛】本题主要考查了复数的四则运算,以及复数的表示,其中解答中熟记复数的运算法则,准确化简、运算复数是解答的关键,着重考查了推理与运算能力,属于基础题.2.设 m 为给定的一个实常数,命题 p:,则“”是“命题 p 为真命题”的( )A. 充分不必要条件 B. 必要不充分条件C. 充分且必要条件 D. 既不充分也不必要条件【答案】A【解析】【分析】由图命题 为真,求得,又由成立时,是成立的,即可得到“”是“命题为真命题”的充分不必要条件,得到答案.【详解】若命题 为真,则对任意恒成立,所以,即.因为成立时,是成立的,所以“”是“命题 为真命题”的充分不必要条件.选 A.【点睛】本题主要考查了全称命题的应用,以及充分不必要条件的应用,其中解答中熟记二次函数的性质,求得恒成立时 的取值范围,进而利用充要条件的判定方法求解是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.3.若等差数列的前 5 项之和,且,则( )A. 12 B. 13 C. 14 D. 15【答案】B【解析】试题分析:由题意得,,又,则,又,所以等差数列的公差为,所以.考点:等差数列的通项公式.【此处有视频,请去附件查看】4.已知某 7 个数的平均数为 3,方差为 ,现又加入一个新数据 3,此时这 8 个数的平均数为x,方差为 ,则( )A. , B. , C. , D. ,【答案】B【解析】【分析】由题设条件,利用平均数和方差的计算公式,进行求解,即可得到答案.【详解】由题意,根据这 7 个数的平均数为 3,方差为 ,即,,即,现又加入一个新数据 3,此时这 8 个数的平均数为,方差为,即,故选 B.【点睛】本题主要考查了数据的平均数和方差的计算公式的应用,其中解答中熟记熟记的平均数和方差的计算公式,准确运算是解答的关键,着重考查了推理与运算能力,属于基础题.5.若正整数 N 除以正整数 m 后的余数为 r,则记为 N=r(mod m)...