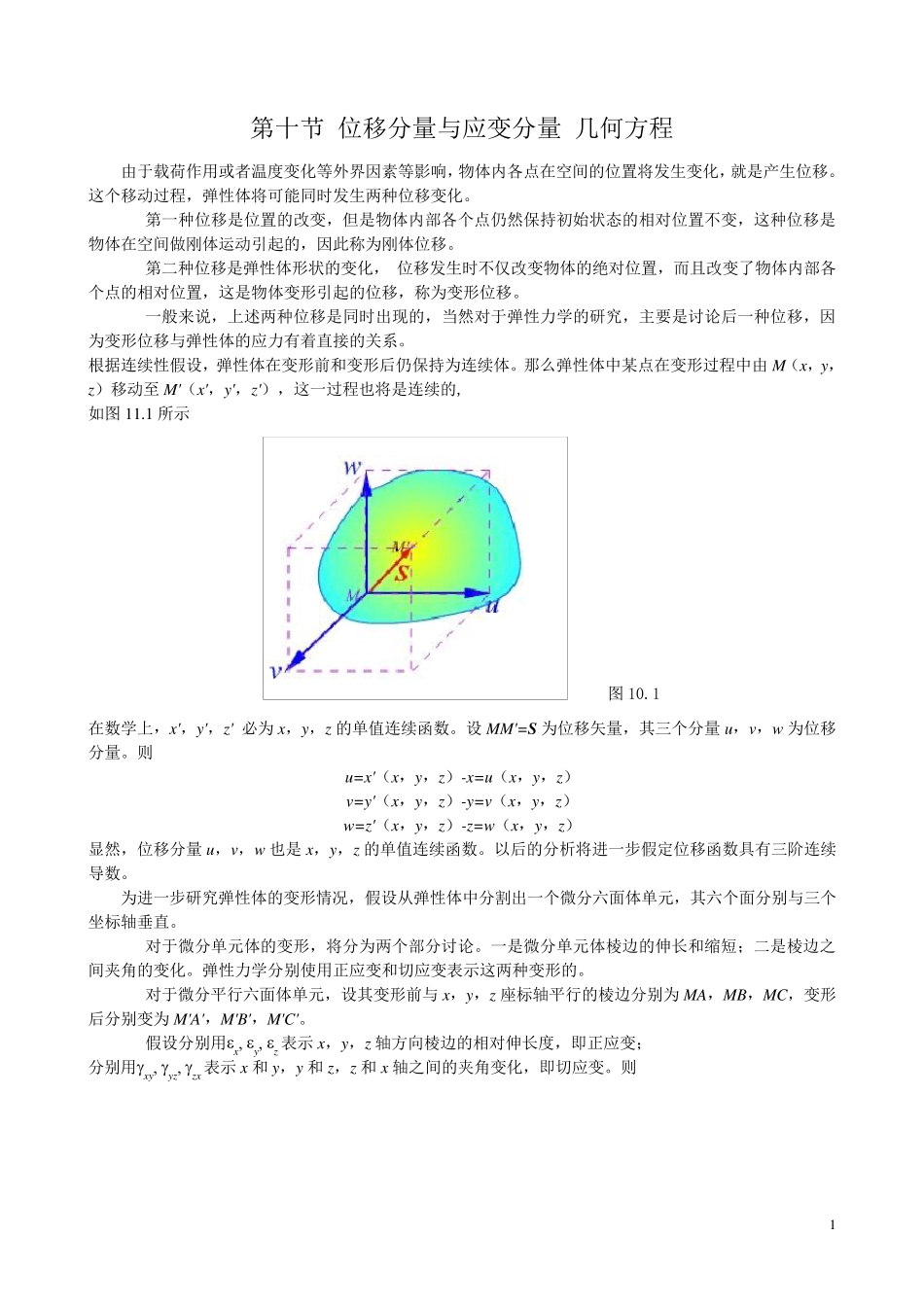
1 第十节 位移分量与应变分量 几何方程 由于载荷作用或者温度变化等外界因素等影响,物体内各点在空间的位置将发生变化,就是产生位移。这个移动过程,弹性体将可能同时发生两种位移变化。 第一种位移是位置的改变,但是物体内部各个点仍然保持初始状态的相对位置不变,这种位移是物体在空间做刚体运动引起的,因此称为刚体位移。 第二种位移是弹性体形状的变化, 位移发生时不仅改变物体的绝对位置,而且改变了物体内部各个点的相对位置,这是物体变形引起的位移,称为变形位移。 一般来说,上述两种位移是同时出现的,当然对于弹性力学的研究,主要是讨论后一种位移,因为变形位移与弹性体的应力有着直接的关系。 根据连续性假设,弹性体在变形前和变形后仍保持为连续体。那么弹性体中某点在变形过程中由M(x,y,z)移动至M'(x',y',z'),这一过程也将是连续的, 如图1 1 .1 所示 图10.1 在数学上,x',y',z' 必为 x,y,z 的单值连续函数。设 MM'=S 为位移矢量,其三个分量u,v,w 为位移分量。则 u=x'(x,y,z)-x=u(x,y,z) v=y'(x,y,z)-y=v(x,y,z) w=z'(x,y,z)-z=w(x,y,z) 显然,位移分量u,v,w 也是x,y,z 的单值连续函数。以后的分析将进一步假定位移函数具有三阶连续导数。 为进一步研究弹性体的变形情况,假设从弹性体中分割出一个微分六面体单元 ,其六个面分别 与三个坐 标 轴 垂 直。 对于微分单元 体的变形,将分为两个部分讨论。一是微分单元 体棱 边 的伸 长 和缩 短 ; 二是棱 边 之间夹 角 的变化。弹性力学分别 使 用正 应变和切 应变表 示这两种变形的。 对于微分平 行 六面体单元 ,设其变形前与x,y,z 座 标 轴 平 行 的棱 边 分别 为 MA,MB,MC,变形后分别 变为 M'A',M'B',M'C'。 假设分别 用xyz表 示x,y,z 轴 方向 棱 边 的相对伸 长 度,即 正 应变; 分别 用 xy yz zx 表 示x 和 y,y 和 z,z 和 x 轴 之 间的夹 角 变化,即 切 应变。则 2 对于小变形问题,为了简化分析,将微分单元体分别投影到Oxy,Oyz,Ozx 平面来讨论。 显然,单元体变形前各棱边是与坐标面平行的,变形后棱边将有相应的转动,但我们讨论的是小变形问题,这种转动所带来的影响较小。特别是物体位移中不影响变形的计算,假设各点的位移仅为自身的大小和形状的变化所确定...