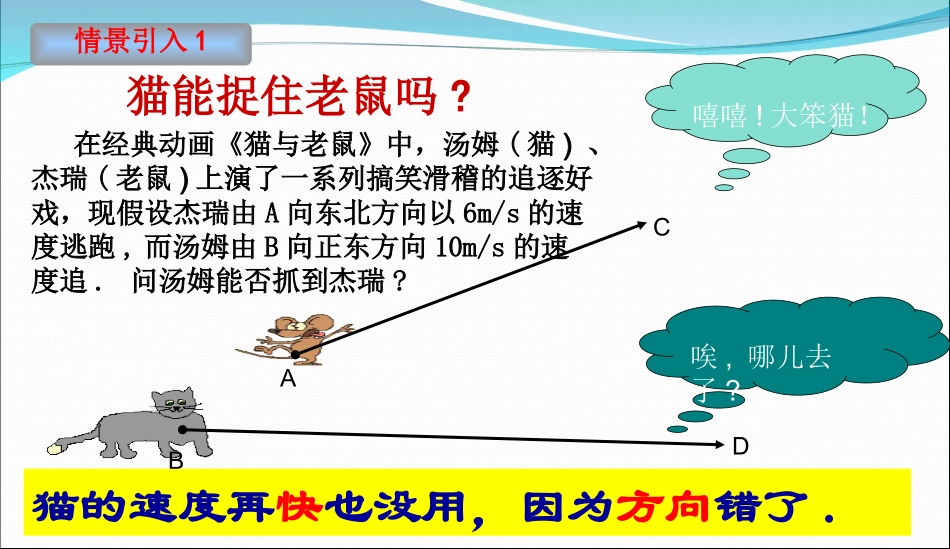
第二章平面向量小结(第1课时)秭归一中梅杰唉,哪儿去了?嘻嘻!大笨猫!BA猫能捉住老鼠吗?在经典动画《猫与老鼠》中,汤姆(猫)、杰瑞(老鼠)上演了一系列搞笑滑稽的追逐好戏,现假设杰瑞由A向东北方向以6m/s的速度逃跑,而汤姆由B向正东方向10m/s的速度追.问汤姆能否抓到杰瑞?CD情景引入1猫的速度再快也没用,因为方向错了.作为值周班校门值岗的同学,在学校门口碰见学生家长询问学校男生公寓的位置,你会告诉家长哪些信息,才能让家长准确找到地方呢?距离的大小和方向想一想情景引入2由于向量概念的双重性,大大冲击了我们以前基于数量的认识。如何认识它,它又如何运算,如何应用它?一系列的困惑使得我们很多同学学习向量时糊涂、迷茫、害怕……“想说爱它不容易”思考:结合本章目录,想一想我们学习本章的流程是怎样的?每一步分别学习了哪些知识?试着完成结构图。知识梳理知识结构力、位移、速度等既有大小又有方向的量几何表示字母表示坐标表示线性运算数量积加法运算减法运算数乘运算几何应用物理应用背景及概念平面向量表示方法运算应用重难点再现剖析b=λa(λR,a≠0∈)ab∥向量表示:坐标表示:设a=(x1,y1),b=(x2,y2),则ab∥x1y2-x2y1=0(1)共线定理:向量a(a≠0)与b共线,当且仅当有唯一一个实数λ,使b=λa.两个重要定理例1.如右图,在ABC中,P为AB边上一点,且满足BP=2AP,已知A点坐标(1,1),B点坐标(-2,-1)1.如何用向量来描述点P的位置?PCBA2.点P的坐标能否用A、B两点的坐标来求解?如何求解?两个重要定理变式:假设点P为线段AB上的一动点,如何用向量来描述点P的位置?PCBA两个重要定理(2)平面向量就基本定理:若e1、e2是同一平面内的两个不共线向量,则对于这一平面内的任意向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2.不共线的向量e1、e2叫做表示这一平面内所有向量的一组基底λ1e1+μ1e2=λ2e1+μ2e2λ1=λ2μ1=μ2向量相等的充要条件两个重要定理3.向量CP能否用CA、CB来表示?如何表示?PCBA变式:向量CP能否用AB、AC来表示?如何表示?在平面直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量i、j作为基底,对于平面内的一个向量a,由平面向量基本定理知,有且只有一对实数x、y,使得a=xi+yj.我们把有序数对(x,y)叫做向量a的坐标,记作a=(x,y).aixyOjxy两个重要定理平面向量有序数对(x,y)平面上点对应对应两个重要定理平面向量基本定理的重要意义平面向量基本定理是向量坐标表示的理论基础平面向量基本定理是向量实现代数化运算的理论支撑两种重要运算形式例2、在平行四边形ABCD中,AD=1,∠BAD=60O,E为CD的中点,若1BEAC,则AB的长为_____________EDCAB总结反思通过学习,我们对向量有了哪些新的认识,对本章知识是否有了一个整体、系统的了解,有哪些知识、方法上的收获?知识:方法:课外活动1.教材118页,复习参考题A组2.【研究性学习课题】写篇小论文:向量作为一种既有大小又有方向的量,结合相关概念和运算,类比我们学习过的实数的运算,试着谈谈它们有什么异同?数形结合思想是高中数学的重要数学思想———数因形而直观、形因数而准确。平面向量作为代数与几何的纽带,素有“与解几交汇,与立几联姻,与代数牵手”的美称,起到数形结合的目的。“慢慢爱上它”