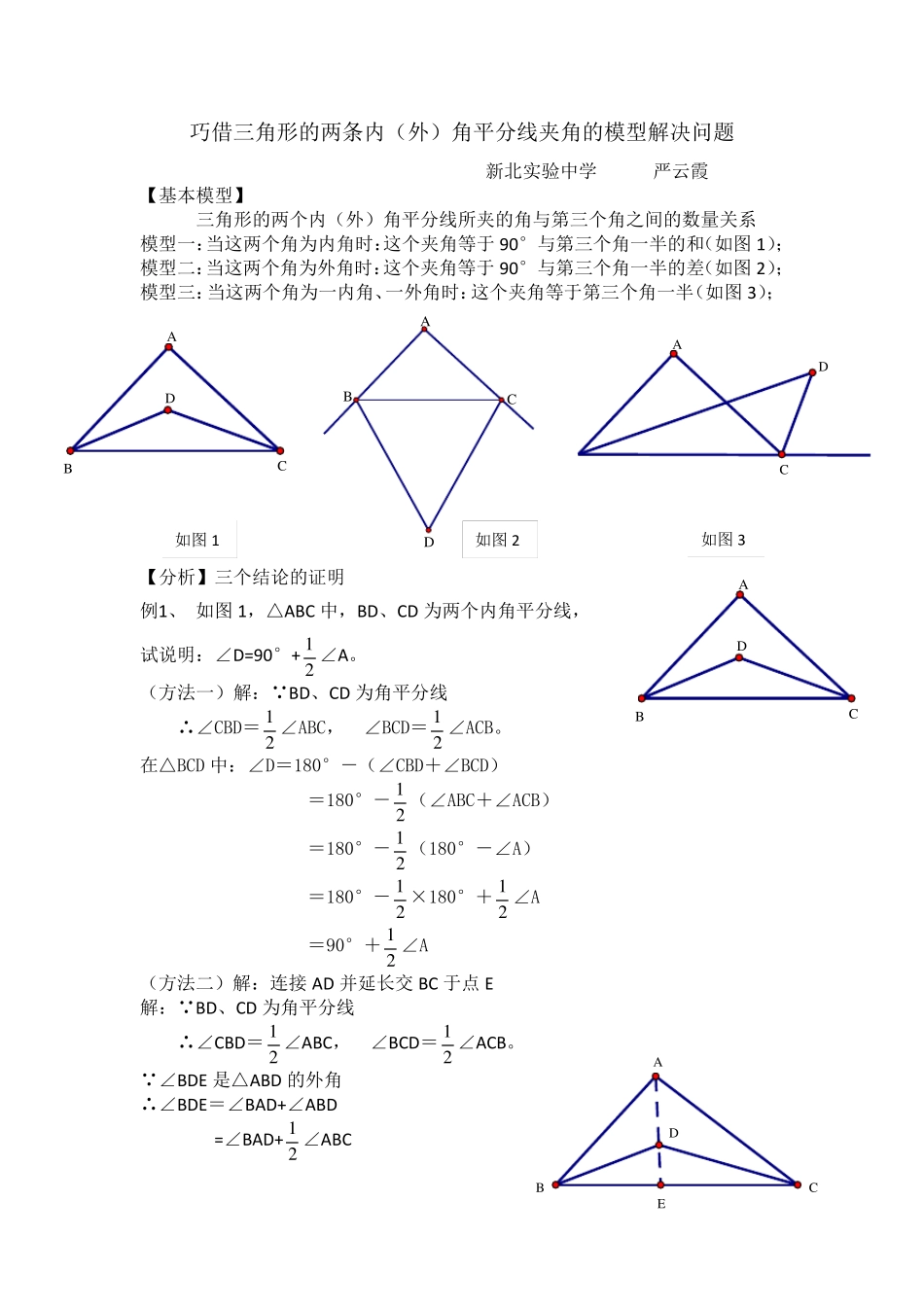
DCAABCDDCBAABCDEDCBA巧借三角形的两条内(外)角平分线夹角的模型解决问题 新北实验中学 严云霞 【基本模型】 三角形的两个内(外)角平分线所夹的角与第三个角之间的数量关系 模型一:当这两个角为内角时:这个夹角等于90°与第三个角一半的和(如图 1); 模型二:当这两个角为外角时:这个夹角等于90°与第三个角一半的差(如图 2); 模型三:当这两个角为一内角、一外角时:这个夹角等于第三个角一半(如图 3); 【分析】三个结论的证明 例1、 如图 1,△ABC 中,BD、CD 为两个内角平分线, 试说明:∠D=90°+ 21 ∠A。 (方法一)解: BD、CD 为角平分线 ∴∠CBD= 21 ∠ABC, ∠BCD= 21 ∠ACB。 在△BCD 中:∠D=180°-(∠CBD+∠BCD) =180°- 21 (∠ABC+∠ACB) =180°- 21 (180°-∠A) =180°- 21 ×180°+ 21 ∠A =90°+ 21 ∠A (方法二)解:连接 AD 并延长交 BC 于点 E 解: BD、CD 为角平分线 ∴∠CBD= 21 ∠ABC, ∠BCD= 21 ∠ACB。 ∠BDE是△ABD 的外角 ∴∠BDE=∠BAD+∠ABD =∠BAD+ 21 ∠ABC 如图 1 如图 2 如图 3 同理可得∠CDE=∠CAD+ 21 ∠ACB 又 ∠BDC=∠BDE+∠CDE ∴∠BDC=∠BAD+ 21 ∠ABC+∠CAD+ 21 ∠ACB =∠BAC+ 21 (∠ABC+∠ACB) =∠BAC+ 21 (180°-∠BAC) =90°+ 21 ∠BAC 例2、如图,BD、CD为△ABC的两条外角平分线, 试说明:∠D=90°- 21 ∠A。 解: BD、CD 为角平分线 ∴∠CBD= 21 ∠CBE ∠BCD=21 ∠BCF 又 ∠CBE、∠BCD 为△ABC 的外角 ∴∠CBE=∠A+∠ACB ∠BCF=∠A+∠ABC ∴∠CBE+∠BCF=∠A+∠ACB+∠A+∠ABC=∠A+180° 在△BCD 中:∠D=180°-(∠CBD+∠BCD) =180°-(21 ∠CBE+ 21 ∠BCF) =180°- 21 (∠CBE+∠BCF) =180°- 21 (∠A+180°) =90°- 21 ∠A 【小结】通过对模型 1、2 的分析和证明,我们还能发现三角形两内角平分线的夹角和两外角平分线的夹角互补,即和为 180°。 例3:如图,在△ABC 中,BD 为∠ABC 的平分线,CD 为∠ACE的平分线,试说明:∠D=21 ∠A; 解: BD 为角平分线, ∴∠CBD=21 ∠ABC, 又 CD 为∠ACE 的平分线 ∴∠DCE= 21 ∠ACE, DCBA而∠DCE 为△BCD 的一个外角 ∴∠DCE=∠D+∠DBC, 即∠D=∠DCE-∠DBC ∴∠D=21 ∠ACE-2...