函数的零点和方程的解VIP免费

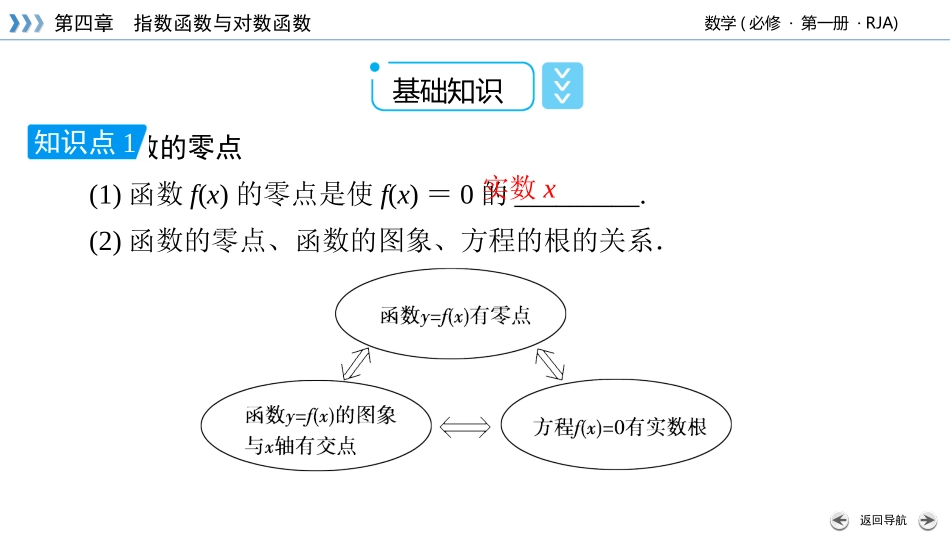
4.5.1函数的零点与方程的解返回导航第四章指数函数与对数函数数学(必修·第一册·RJA)函数的零点(1)函数f(x)的零点是使f(x)＝0的_________.(2)函数的零点、函数的图象、方程的根的关系．实数x基础知识知识点1返回导航第四章指数函数与对数函数数学(必修·第一册·RJA)思考1：(1)函数的零点是点吗？(2)函数的零点个数、函数的图象与x轴的交点个数、方程f(x)＝0根的个数有什么关系？提示：(1)不是，是使f(x)＝0的实数x，是方程f(x)＝0的根．(2)相等．返回导航第四章指数函数与对数函数数学(必修·第一册·RJA)函数的零点存在定理(1)条件：函数y＝f(x)在区间[a，b]上的图象是__________________，f(a)f(b)<0；(2)函数y＝f(x)在区间(a，b)上有零点，即存在c(∈a，b)使f(c)＝0，这个c也就是f(x)＝0的根．连续不断的曲线知识点2返回导航第四章指数函数与对数函数数学(必修·第一册·RJA)C基础自测1．函数f(x)＝4x－6的零点是()A．23B．(32，0)C．32D．－32[解析]令4x－6＝0，得x＝32，∴函数f(x)＝4x－6的零点是32.返回导航第四章指数函数与对数函数数学(必修·第一册·RJA)2．(2020·广州荔湾区高一期末测试)函数f(x)＝x－2＋log2x，则f(x)的零点所在区间为()A．(0,1)B．(1,2)C．(2,3)D．(3,4)[解析]f(1)＝－1＋log21＝－1，f(2)＝log22＝1，∴f(1)·f(2)<0，故选B．B返回导航第四章指数函数与对数函数数学(必修·第一册·RJA)3．若函数f(x)＝x2＋2x＋a没有零点，则实数a的取值范围是()A．a＜1B．a＞1C．a≤1D．a≥1[解析]函数f(x)＝x2＋2x＋a没有零点，即方程x2＋2x＋a＝0没有实数根，所以Δ＝4－4a＜0，得a＞1.B返回导航第四章指数函数与对数函数数学(必修·第一册·RJA)4．二次函数y＝ax2＋bx＋c中，a·c<0，则函数有_____个零点．[解析]令ax2＋bx＋c＝0，Δ＝b2－4ac， a·c<0，∴b2－4ac>0，∴方程ax2＋bx＋c＝0有两个不相等实根，∴二次函数y＝ax2＋bx＋c(a·c<0)有2个零点．2返回导航第四章指数函数与对数函数数学(必修·第一册·RJA)关键能力·攻重难返回导航第四章指数函数与对数函数数学(必修·第一册·RJA)题型一求函数的零点(方程的根)题型探究例1判断下列函数是否存在零点，如果存在，请求出．(1)f(x)＝－x2－4x－4；(2)f(x)＝x－1x2－4x＋3x－3；(3)f(x)＝4x＋5；(4)f(x)＝log3(x＋1)．返回导航第四章指数函数与对数函数数学(必修·第一册·RJA)[分析]求函数的零点，就是求相应方程的实数根．[解析](1)令－x2－4x－4＝0，解得x＝－2，所以函数f(x)存在零点，且零点为x＝－2.(2)令x－1x2－4x＋3x－3＝0，解得x＝1，所以函数f(x)存在零点，且零点为x＝1.返回导航第四章指数函数与对数函数数学(必修·第一册·RJA)(3)令4x＋5＝0，显然方程4x＋5＝0无实数根，所以函数f(x)不存在零点．(4)令log3(x＋1)＝0，解得x＝0，所以函数f(x)存在零点，且零点为x＝0.返回导航第四章指数函数与对数函数数学(必修·第一册·RJA)[归纳提升]1.正确理解函数的零点：(1)函数的零点是一个实数当自变量取该值时，其函数值等于零．(2)根据函数零点定义可知函数y＝f(x)的零点⇔方程f(x)＝0的实根⇔函数y＝f(x)的图象与x轴交点的横坐标．2．函数零点的求法：(1)代数法：求方程f(x)＝0的实数根．(2)几何法：与函数y＝f(x)的图象联系起来，图象与x轴的交点的横坐标即为函数的零点．返回导航第四章指数函数与对数函数数学(必修·第一册·RJA)【对点练习】❶(1)求下列函数的零点：①f(x)＝x2－2x－3零点为__________；②g(x)＝lgx＋2零点为______.(2)已知－1和4是函数f(x)＝ax2＋bx－4的零点，则f(1)＝_______.[解析](1)①f(x)＝(x－3)·(x＋1)，令f(x)＝0，得x1＝－1，x2＝3，∴f(x)的零点为3和－1，3，－1－61100返回导航第四章指数函数与对数函数数学(必修·第一册·RJA)②由lgx＋2＝0得，lgx＝－2，∴x＝1100.故g(x)的零点为1100.(2)由条件知f－1＝0f4＝0，∴a－b－4＝016a＋4b－4＝0，∴a＝1b＝－3，∴f(1)＝a＋b－4＝－6.返回导航第四章指数函数与对数函数数学(必修·第一册·RJA)(2020·江西宜丰中学高一期末测试)函数f(x)＝lnx＋x3－9的...