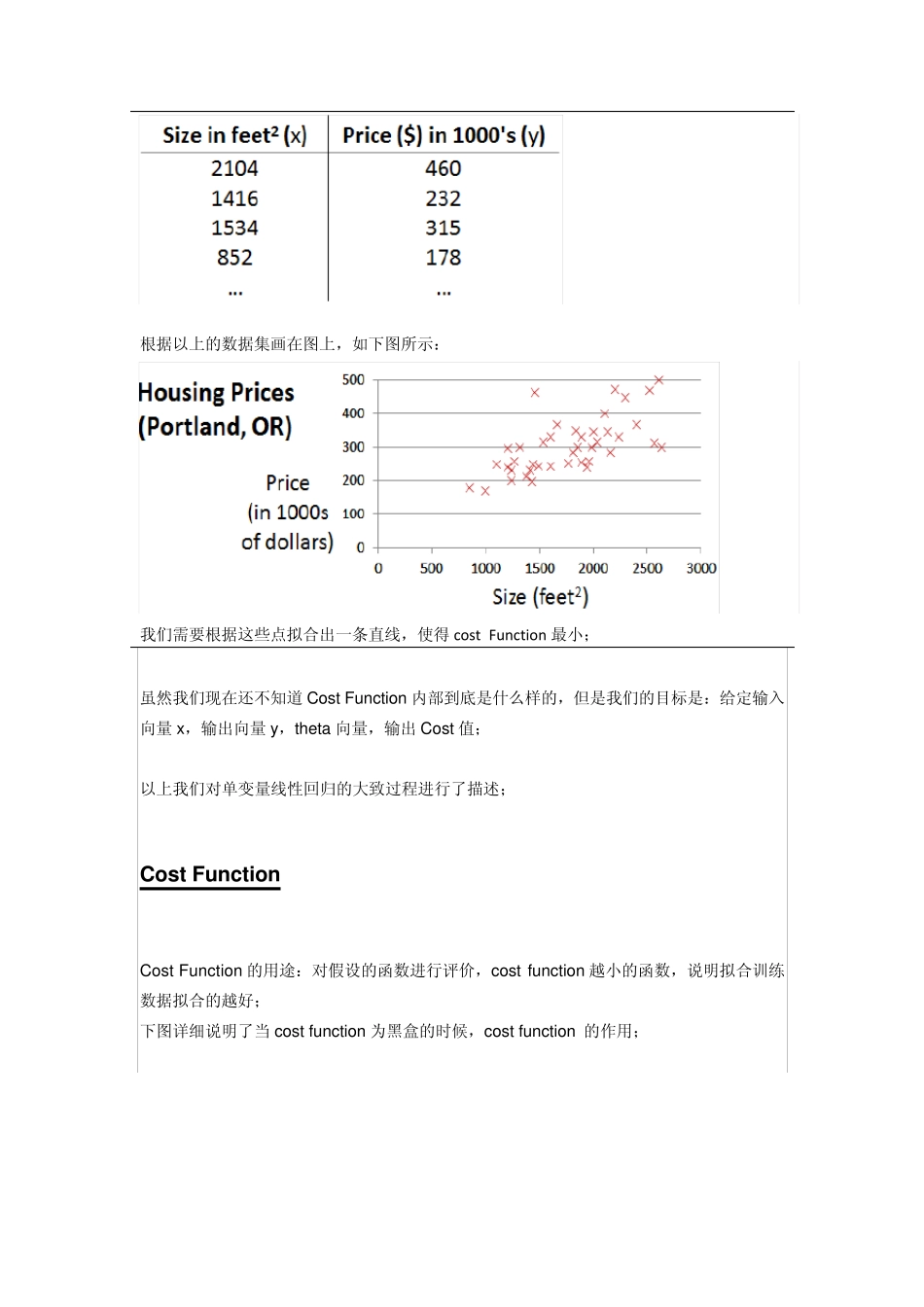
本文会讲到: (1)线性回归的定义 (2)单变量线性回归 (3)cost function:评价线性回归是否拟合训练集的方法 (4)梯度下降:解决线性回归的方法之一 (5)feature scaling:加快梯度下降执行速度的方法 (6)多变量线性回归 Linear Regres s ion 注意一句话:多变量线性回归之前必须要 Feature Scaling! 方法:线性回归属于监督学习,因此方法和监督学习应该是一样的,先给定一个训练集,根据这个训练集学习出一个线性函数,然后测试这个函数训练的好不好(即此函数是否足够拟合训练集数据),挑选出最好的函数(cost function 最小)即可; 注意: (1)因为是线性回归,所以学习到的函数为线性函数,即直线函数; (2)因为是单变量,因此只有一个 x; 我们能够给出单变量线性回归的模型: 我们常称 x 为 feature,h(x)为 hypothesis; 从上面“方法”中,我们肯定有一个疑问,怎么样能够看出线性函数拟合的好不好呢? 我们需要使用到Cost Function(代价函数),代价函数越小,说明线性回归地越好(和训练集拟合地越好),当然最小就是0,即完全拟合; 举个实际的例子: 我们想要根据房子的大小,预测房子的价格,给定如下数据集: 根据以上的数据集画在图上,如下图所示: 我们需要根据这些点拟合出一条直线,使得 cost Fu nction 最小; 虽然我们现在还不知道 Cost Function 内部到底是什么样的,但是我们的目标是:给定输入向量 x,输出向量 y,theta 向量,输出Cost 值; 以上我们对单变量线性回归的大致过程进行了描述; Cost Fu nction Cost Function 的用途:对假设的函数进行评价,cost function 越小的函数,说明拟合训练数据拟合的越好; 下图详细说明了当 cost function 为黑盒的时候,cost function 的作用; 但是我们肯定想知道cost Function 的内部构造是什么?因此我们下面给出公式: 其中: 表示向量x 中的第i 个元素; 表示向量y 中的第i 个元素; 表示已知的假设函数; m 为训练集的数量; 比如给定数据集(1,1)、(2,2)、(3,3) 则 x = [1;2;3],y = [1;2;3] (此处的语法为Octave语言的语法,表示3*1的矩阵) 如果我们预测 theta0 = 0,theta1 = 1,则 h(x) = x,则 cost function: J(0,1) = 1/(2*3) * [(h(1)-1)^2+(h(2)-2)^2+(h(3)-3)^2] = 0; 如果我们预测 theta0 = 0,theta1 = 0.5,则 h(x) = 0.5x,则 cost f...