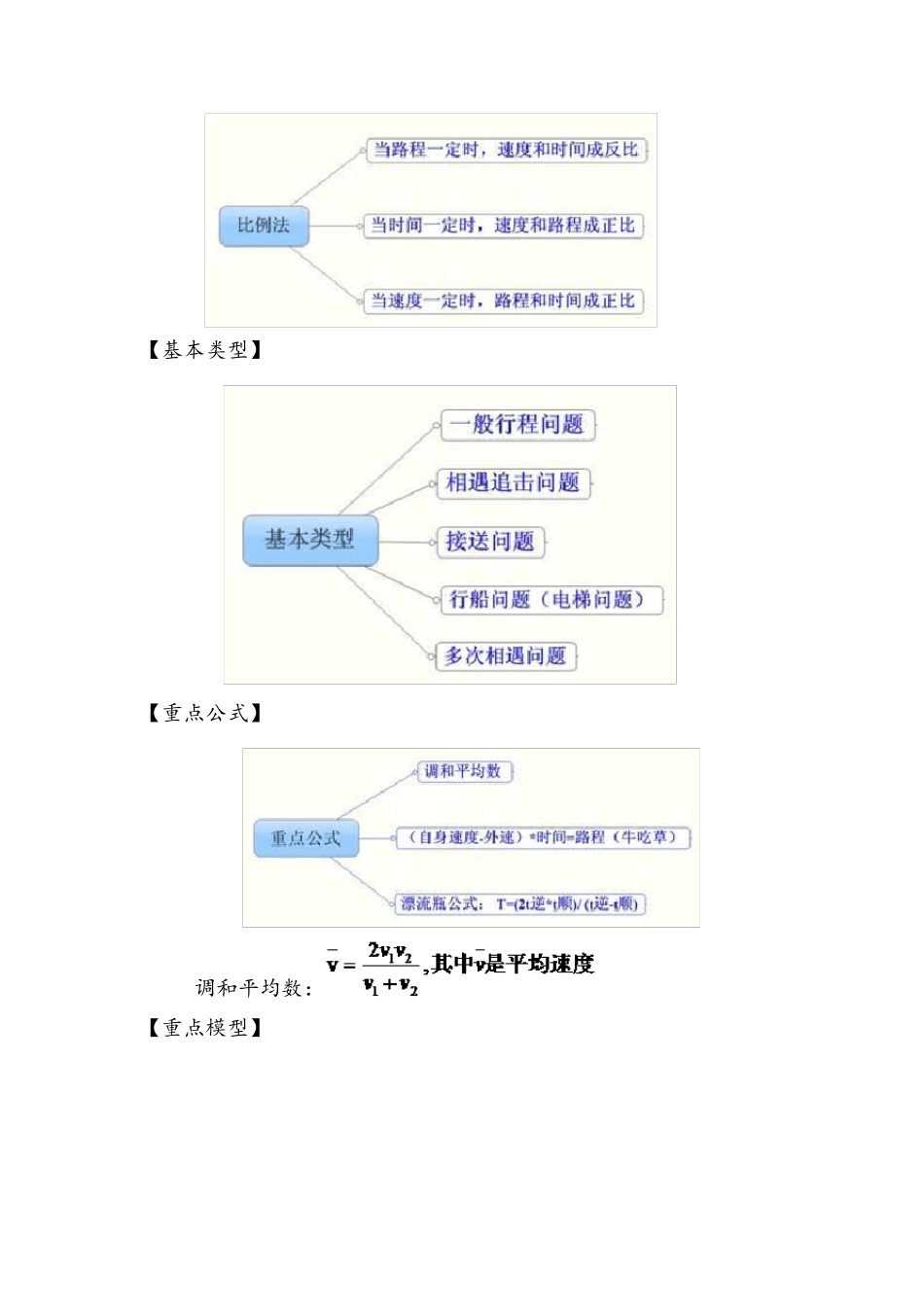
行 程 问 题 【知识框架】 【核心点拨】 不便应万变的神器: 路程=速度*时间 S=v *t 【解题方法】 比例法是解决行程问题最简捷最有效的方法,灵活运用好比例法不但能解决处理好行程问题,更是攻克数学运算的一件法宝。 【基本类型】 【重点公式】 调和平均数: 【重点模型】 1、相遇问题模型 两车分别从 A、B 两地出发,并在 A、B 两地间不间断往返行驶的多次相遇问题,关键就是速度比和路程的倍数关系 第一次相遇,两人共走了 1S 第二次相遇,两人共走了 3S 第三次相遇,两人共走了 5S .............. 第 N 次相遇,两人共走了 2*N-1 个 S,经过了 2*N-1 个相遇时间 “为什么第二次相遇走了 3 个相遇时间?为什么不是 2 个相遇时间?”。下面我来推导下这个问题 第一次甲走的:AC 乙走的是 BC 甲乙第一次相遇 1 个相遇时间 t内共走了 1S. 第二次相遇时,甲走了AC+CB+BD------------------① 乙走了BC+CA+AD------------------② ①+②=3S (甲乙共走了3S) 甲乙第一次相遇共走了1S,1t 甲乙第二次相遇共走了3S,因为速度不变,所以走的时间为3t 推广下成公式: 第N 次相遇,甲乙共走了(2N-1)个S,花了(2N-1)个相遇时间t 备注:对于单个的行程也是适用的,不增加推导 例题:甲.乙两人同时从A、B 两地出发相向而行,甲到达 B 地后立即往回走,回到 A 地后,又立即向 B 地走去;已到达 A 地后立即往回走,回到 B 地后,又立即向 A 地走去。如此往复,行走的速度不变,若两人第二次迎面相遇,地点距 A 地 500 米,第四次迎面相遇地点距 B 地 700 米,则 A、B 两地的距离是( ) A.1460 米 B.1350 米 C.1300 米 D.1120 米 【幕王侧解析】第四次走了7s 正好离 b700 7 倍数 锁 D 2、单双岸模型 第一次相遇时距离是S1,第二次相遇距离是S2 全程S 如果S1、S2 相对的是一个地点则为单岸型,否则为双岸型 单岸型公式:S=(3S1+S2)/2 双岸型公式:S=3S1-S2 例题:甲从 A 地,乙从 B 地同时以均匀的速度相向而行,第一次相遇离A 地 6 千米,继续前进,到达对方起点后立即返回,在离B地 3 千米处第二次相遇,则 A、B 两地相距多少千米? A.10 B.12 C.18 D.15 【幕王侧解析】本题属于双岸问题,直接套公式。 3*6-3=15 3、接送问题模型 某团体从甲地到乙地,甲、乙两地相距100 千米,团体中一部分人乘车先行,余下的人步行,...